核心套路
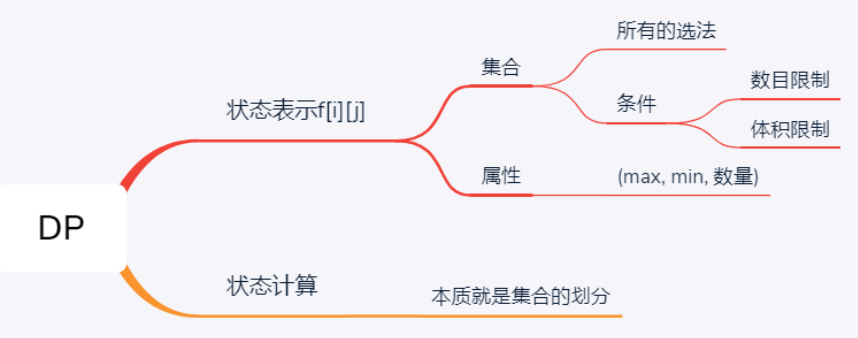
优化一般就是优化状态转移方程
01背包
特点:每个物品仅能使用一次
重要变量&公式解释
f[i][j]:表示所有选法集合中,只从前i个物品中选,并且总体积≤j的选法的集合,它的值是这个集合中每一个选法的最大值.
状态转移方程
f[i][j] = max(f[i-1][j], f[i-1][j-v[i]]+w[i])
f[i-1][j]:不选第i个物品的集合中的最大值
f[i-1][j-v[i]]+w[i]:选第i个物品的集合,但是直接求不容易求所在集合的属性,这里迂回打击一下,先将第i个物品的体积减去,求剩下集合中选法的最大值.
问题
集合如何划分
-
一般原则:不重不漏,不重不一定都要满足(一般求个数时要满足)
-
如何将现有的集合划分为更小的子集,使得所有子集都可以计算出来.
//无优化版
#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main() {
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++) {
for(int j = 0; j <= m; j++) {
f[i][j] = f[i-1][j];
if(j>=v[i]) f[i][j] = max(f[i][j], f[i-1][j-v[i]]+w[i]);
}
}
cout << f[n][m] << endl;
return 0;
}
//有优化版
/*
1. f[i] 仅用到了f[i-1]层,
2. j与j-v[i] 均小于j
3.若用到上一层的状态时,从大到小枚举, 反之从小到大哦
*/
#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main() {
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = m; j >= v[i]; j--)
f[j] = max(f[j], f[j-v[i]]+w[i]);
cout << f[m] << endl;
return 0;
}


已经把DP的精髓总结出来了,很不错!
被闫哥夸了hhh,开心!!!
主页爆了y总
能不能把f[i-1][j]:不选第i个物品的集合中的最大值和选这个物品,调换一下位置呢?大佬
逻辑我都明白了但是我真的不知道值是哪里来的,比如f[4][5]的值是8,f[N][N]不是一个定义的二维数组吗,他哪里来的值哦
对我也想知道
通过if(j>=v[i]) f[i][j] = max(f[i][j], f[i-1][j-v[i]]+w[i]);来实现值的
两重循环来覆盖,+w[i]来实现值的变化
他这个std里面的全局变量默认赋值为0?
唉 好难啊,能看懂状态转移方程是啥意思,但是始终体会不到为什么要这样想。。
多写两次就记住了
牛逼
f[i][j] = f[i-1][j];
if(j>=v[i])
f[i][j] = max(f[i][j], f[i-1][j-v[i]]+w[i]);
第一行不是已经让f[i][j]=f[i-1][j] 了吗,为什么后面 max中还要i-1
集合划分部分有分两种情况,f[i][j] = f[i - 1][j]是从i个物品里面选不包含第i个物品,总体积不超过j的情况等价于从0 ~i - 1个物品里面选,总体积不超过j;f[i][j] = max(f[i][j], f[i-1][j-v[i]]+w[i])则是集合划分的第二种情况,包含第i个物品的情况,然后这两种情况取max就是想要的答案了
牛逼啊铁子,教我吧(来自初学者的膜拜)
可以交流呀,大家一起进步
应该是max(f[i-1][j], f[i-1][j-v[i]]+w[i])叭,可以选vi的情况下,比较选vi(f[i-1][j-v[i]]+w[i])和不选vi(f[i-1][j])函数值的大小
哦哦 好像两个都可以 上一行更新了f[i][j]的值
更新了不就是减去两个1了吗
楼主的代码第一行是让值改变,没有改变i。
i的值没有改变啊,不是i–
大佬,f[i][j] = f[i-1][j];这样能实现得到集合的最大值吗?为啥?
f[i-1][j-v[i]]+w[i]:选第i个物品的集合,但是直接求不容易求所在集合的属性,这里迂回打击一下,先将第i个物品的体积减去,求剩下集合中选法的最大值.
这个有点不太理解,有哪位大佬讲一下
我觉得应该是为了满足max这个筛选的属性,这样才能比较前i-1个物品和前i个物品的最大价值,单纯计算前i个物品的最大价值也不好求(因为只能通过前面求后面,这种更新的方式)
tql朴素版的dp解法差不多能理解了 优化版的还是不大懂 想问问大佬平时做题的话一定要优化嘛
同问
优化版写起来更快,不过一般做DP如果不是板子题基本都是按规矩一步一步写,有时间再优化。很少有DP题目需要去优化才能AC。平常做题掌握就行
01背包中为什么当j>=v[i]的时候就可以装第i个物品了呢,j的意思不是总体积不超过j,如果只是总体积大于v[i],但是背包剩余的体积小于v[i],肯定装不下v[i]啊,求教
因为状态转移方程需要用到j - v[i]
个人理解:
首先f[ i ][ j ]的含义是:从前i个物品当中选(包括第i个物品),所有选择的物品的体积之和不超过背包容量j,且所选得的物品的价值总和最大的一种选法,f[i][j]的值就是这种最优选法对应的价值总和的值
当j >= v[i], f[ i ][ j ] = max(f[ i - 1 ][ j ], f[ i - 1 ][ j - v[ i ] ] + w[ i ])的含义是:
若当前背包的体积j能够装得下当前枚举的物品,也就是j>=v[i]
那么我们现在就有两种选择:装这个物品,不装这个物品
根据前面讲的f[i][j]的含义可知,f[i][j]的值应该取这两种选择中所对应的价值总和的最大值
f[i - 1][j]的含义:不装这个物品
f[i - 1][j - v[i]] + w[i]的含义:装这个物品,为什么是i - 1和j - v[i]呢?
我的理解是:为了保证装这个物品的时候取得了最大值,那么我们就要保证:f[i - 1][j - v[i]]取得了最大值,最大值加上一个值还是最大值,即保证了装这个物品所对应的数组元素的值取得了它能够取得的最大值
最后两种情况的值取max,就得到了f[i][j]的一个最优解
再补充一下后面讲的f[i - 1][j - v[i]], 这个式子出现的前提是:我们打算装当前枚举到的物品,那么我们当前背包的J就包含了当前枚举到的物品的体积v[i]
换一种方式来看问题:我们想要让装这个物品所对应的价值总和最大,那么在装这个物品之前,也就是枚举到当前物品之前,我们就要让f[i - 1][j - v[i]]的值最大,一个最大值加上当前枚举到的物品的价值w[i]之后,还是一个最大值
老哥谢谢你,终于懂了
大佬,我能不能先把执行if语句这个(也就是放进去)放在f[i][j]=f[i-1]][j];上面
为什么不给 f [i] [j] 赋值他就会有值(新手小白,大佬勿笑)
全局变量默认为0
其实这样默认为0是不太好的吧,初始化还是得根据不同背包问题来定?
想问一下为撒前面定义要定义在main函数前面,定义在里面就不行了啊
main函数内的空间也是有限的,数据大的时候开在全局才会开的出来空间,2.全局变量默认为零
第一次写题解,写的不好多提意见hhh.
棒棒哒
#include <bits/stdc++.h> using namespace std; int n, m, w[1005], c[1005], dp[1005][1005]; int main() { cin >> n >> m; for(int i = 1;i <= n;i ++) { cin >> w[i] >> c[i]; } for(int i = 1;i <= n;i ++) { for(int v = m;v > 0;v --) { if(w[i] <= v) { dp[i][v] = max(dp[i - 1][v], dp[i - 1][v - w[i]] + c[i]); } else dp[i][v] = dp[i - 1][v]; } } cout << dp[n][m]; return 0; }小白应该看这些吗?🤔
太简单了
我还是不太懂为什么优化后f[j]=f[j],有大佬能讲一讲么
听君一席话,胜读十年书。
嗨嗨嗨萌新来咯
算法逻辑我都懂,我就是不明白值是哪里来的,比如f[4][5],2维数组不是值都没定义吗,他是哪里来的值啊
我也想知道有了解吗
这个不是状态转移方程里面就有嘛
作为一个菜鸟,在看见这个题目时选择了递归,能算出来满足容量的几种价值的情况,但是由于是递归不是迭代,我的技术限制了我求不出来最大值,向大佬求解
using namespace std;
int N,V;
int a[1000],b[1000];
void f(int sum,int jia,int i)//sum表示物品的体积和,jia表示物品的价值和,i表示物品在数组中的下标
{
int j;
for(j=1;j<=N;j++)
{
if(sum+a[j][HTML_REMOVED]V)//若是拿了最后一个超出了背包容量就减掉
{jia=jia-b[i];
sum=sum-a[i];
cout<<”jia”<<jia;
return;}
}
if(sum<V&&i<N)//进入递归的条件背包还有空间并且物品还没遍历完
{
//cout<<”a[i]”<<a[i];
f(sum+a[i],jia+b[i],i+1);//拿上了
f(sum,jia,i+1);//漏过去没拿
}
int main()
{
cin>>N>>V;
for(int i=1;i<=N;i++)
{
cin>>a[i];
cin>>b[i];
}
f(0,0,1);
}