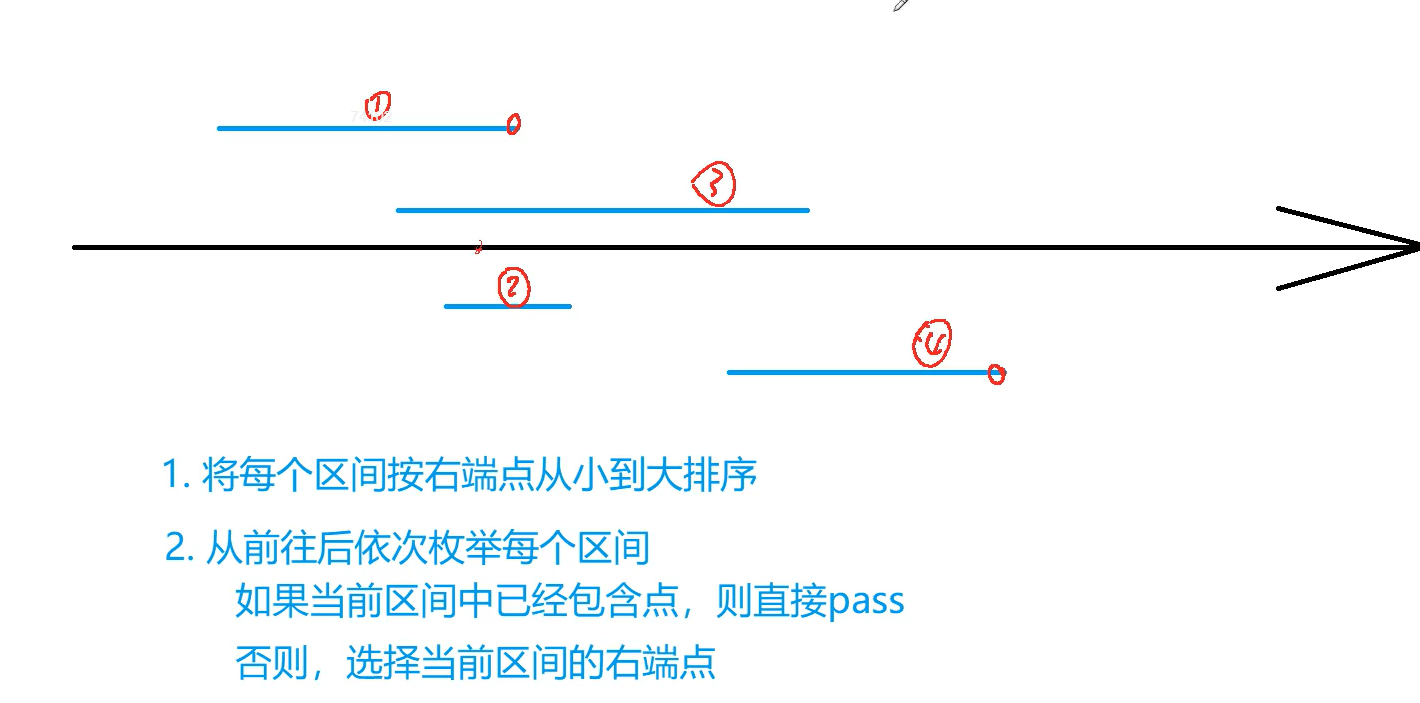
第一个贪心题，有问题的话可以批评指正。

yls在基础课中描述的写贪心题的思路

可以先随便试一下想到的方法（应该要很多的积累吧）
举几个例子，看看自己的算法有没有问题（可以从问题中改进自己的算法）
没有问题之后，尝试证明自己的算法的正确性（感觉这一步有点难）

下面这个题目是yls讲的例子

题目描述

给定 N 个闭区间 [ai,bi]，请你在数轴上选择尽量少的点，使得每个区间内至少包含一个选出的点。

输出选择的点的最小数量。

位于区间端点上的点也算作区间内。

输入格式
第一行包含整数 N，表示区间数。

接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两个端点。

输出格式
输出一个整数，表示所需的点的最小数量。

数据范围
1≤N≤105,
−109≤ai≤bi≤109

样例

输入样例：

3
-1 1
2 4
3 5

输出样例：

2

• 这道题目yls的思路
  

• 使用这个思路验证样例，发现满足条件，之后再证明这个思路的正确性
  

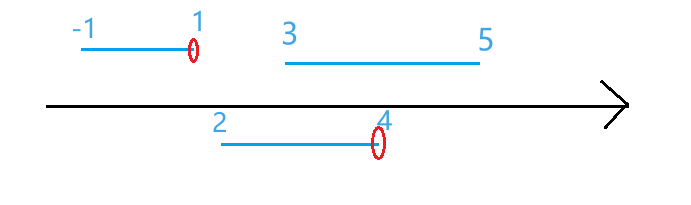
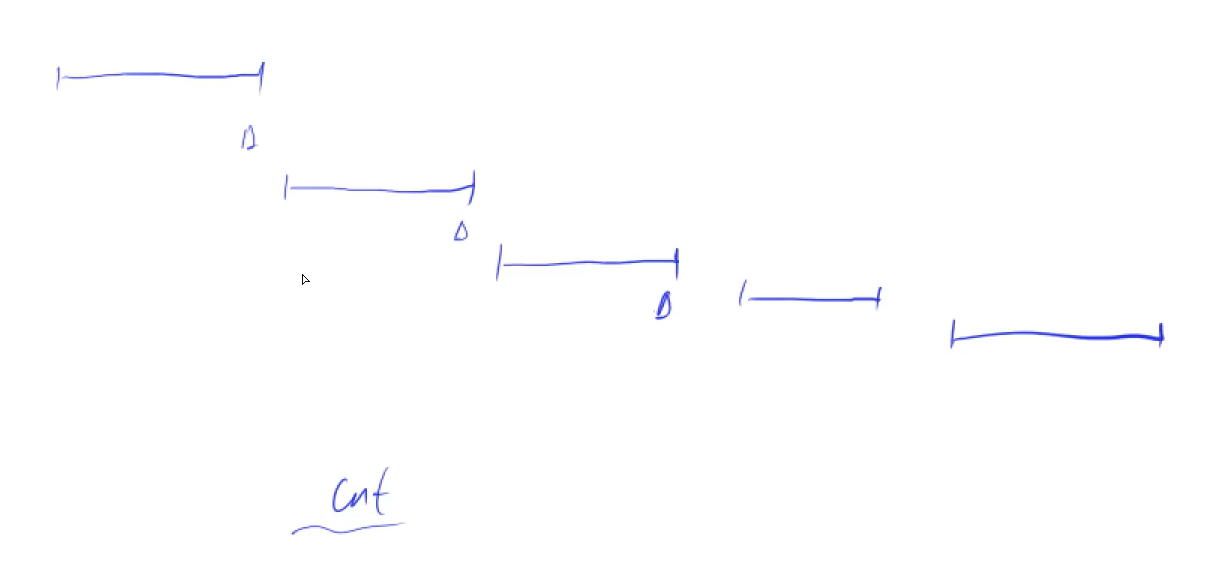
• 证明思路的正确性
  要证明思路的正确性，可以通过证明cnt == ans， cnt表示使用这个思路求出来的满足条件的点数，ans表示选的最少的点的数量
  要证cnt == ans, 只需证cnt >= ans且cnt <= ans
  证明cnt >= ans,因为ans为最小值，显然有cnt >= ans成立
  证明cnt <= ans:
  假设有cnt个相互之间没有任何交集的区间，如果想要把cnt个区间都覆盖的话，则最少需要cnt个点，对于所有可行的方案都需要>=cnt，则有ans >= cnt，因为ans一定为可行的方案。
  

代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int n;
struct Range
{
    int l, r;
    // 根据右端点排序，需要重载小于运算符
    bool operator< (const Range &w) const
    {
        return r < w.r;
    }
}range[N];

int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++) scanf("%d%d", &range[i].l, &range[i].r);

    // 根据右端点对区间进行排序
    sort(range, range + n);

    // ed表示上一个点的下标
    int res = 0, ed = -2e9;
    for (int i = 0; i < n; i ++)
    // 当前区间的左端点严格大于ed，选择一个新的点
        if (range[i].l > ed)
        {
            res ++;
            ed = range[i].r;
        }

    cout << res << endl;

    return 0;
}

因为太菜了，对int的范围有点不清楚，所以记录一下
int的范围大概为-2e9 ~ 2e9