分析

• 每一行都是一个单词，需要在所有给定的单词中进行匹配，可以认为模板串和待匹配的串是同一组数据。

• 对于所以输入的单词，建立一棵trie树，对于某个单词我们想要统计出其在其他所有（包含自己）串中出现的次数，我们应该怎么统计呢？

• 首先，我们要明确某个单词出现的次数一定小于等于所有字符串的总长度。

• 一个字符串出现的次数=所有满足要求的前缀个数，要求是这个前缀的的后缀等于原串。

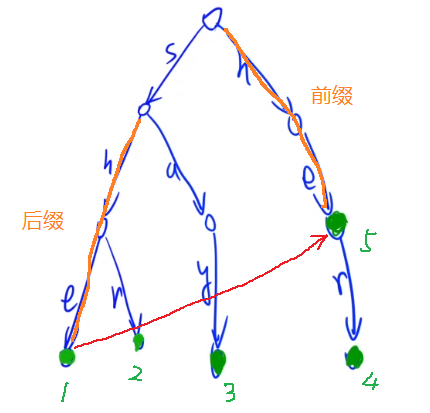
• 这里采用另外一种思路：考虑每一个前缀t，t的后缀等于多少个前缀。相当于反过来考虑，这样一来我们可以迭代求解。

• 对于所有存在的边(i, next[i])，我们都连一条边，则我们会形成一个有向无环图，因为i所在的层一定比next[i]所在的层深。

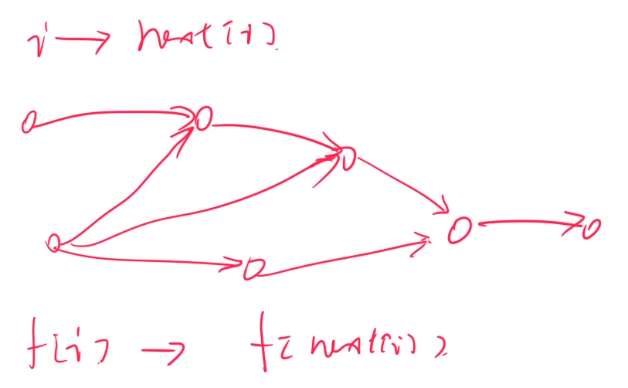
• 上图中f的含义：

（1）建立trie后, f代表当前节点代表的字符串(必须从根节点开始形成的字符串)出现的次数；

（2）依据拓扑序进行递推即可，即f[next[i]]+=f[i]。递推之后, f代表当前节点代表的字符串在整个trie中出现的次数。这个递推过程可以参考上面的原理中的图，如下图：

#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int n;  // 单词个数
int tr[N][26], idx;
// 建立trie后, f代表当前节点代表的字符串(必须从根节点开始形成的字符串)出现的次数
// 递推之后, f代表当前节点代表的字符串在整个trie中出现的次数
int f[N];

int q[N];  // BFS求ne时使用到的队列
int ne[N];
char str[N];  // 输入字符串
int id[210];  // 每个单词在trie中对应节点的编号

void insert(int x) {

    int p = 0;
    for (int i =0; str[i]; i++) {
        int t = str[i] - 'a';
        if (!tr[p][t]) tr[p][t] = ++idx;
        p = tr[p][t];
        f[p]++;  // 每一个结束的位置都代表一个字符串
    }
    id[x] = p;
}

void build() {

    int hh = 0, tt = -1;
    for (int i = 0; i < 26; i++)
        if (tr[0][i])
            q[++tt] = tr[0][i];

    while (hh <= tt) {
        int t = q[hh++];
        for (int i = 0; i < 26; i++) {
            int &p = tr[t][i];
            if (!p) p = tr[ne[t]][i];
            else {
                ne[p] = tr[ne[t]][i];
                q[++tt] = p;
            }
        }
    }
}

int main() {

    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        scanf("%s", str);
        insert(i);  // i是当前单词对应编号
    }

    // 求解ne
    build();
    // 递推更新f, trie中节点编号为0~idx，一共idx+1个点，0既代表根节点又代表空节点
    for (int i = idx; i; i--) f[ne[q[i]]] += f[q[i]];

    for (int i = 0; i < n; i++) printf("%d\n", f[id[i]]);

    return 0;
}