AC自动机原理

• AC自动机：Trie+KMP的组合。

• AC自动机是在KMP的基础上进行扩展，在KMP中，我们存在模式串p以及被匹配的串s，我们可以通过KMP算法在$O(n)$的时间内判断p是否在s中出现过、出现的位置以及出现的次数。AC自动机实质上是将模式串p换成了trie树，为了理解AC自动机，我们需要深入理解KMP算法，关于KMP的算法原理如下：

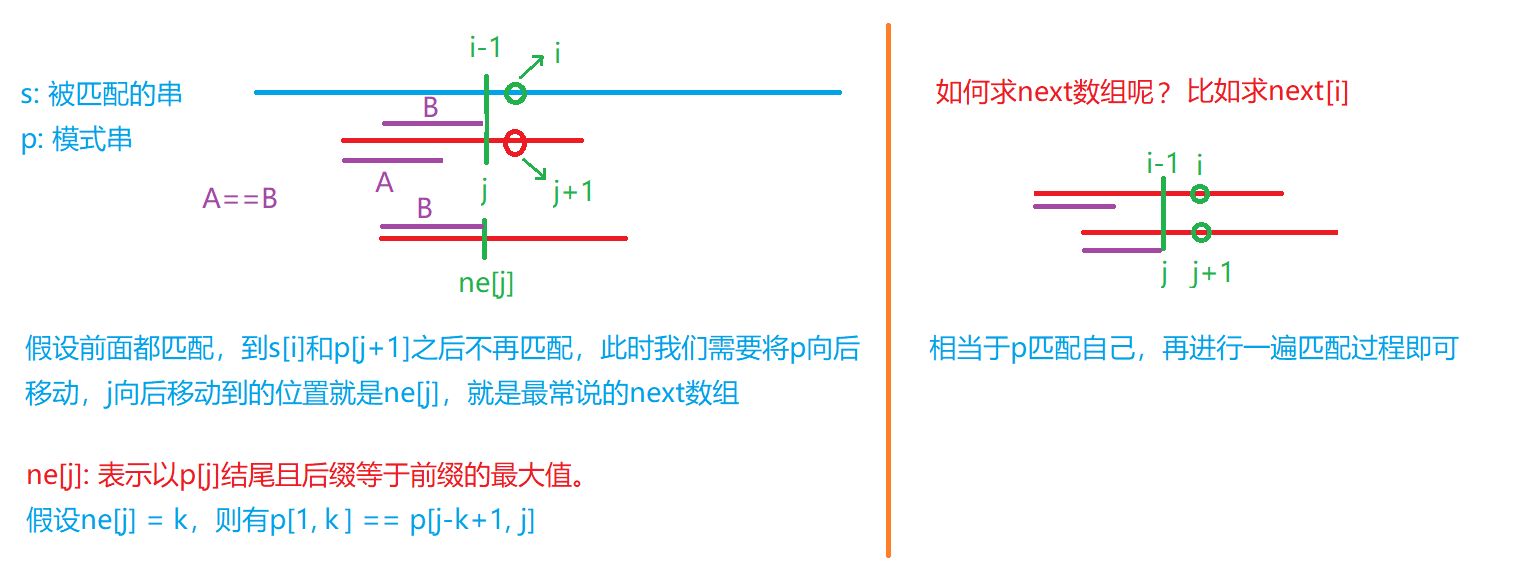
• 这里分析一下一下next数组的求解代码

// 求next数组, ne[1]=0表示如果p[1]没有匹配上，从头开始匹配
for (int i = 2, j = 0; i <= n; i++) {
    // 这里的j起始就是ne[i-1]
    // 因为当i=2时，ne[2-1]=0，符合要求；之后每次循环最后ne[i]被赋值为j，然后i++, 因此ne[i - 1]就是j
    while (j && p[i] != p[j + 1]) j = ne[j];
    if (p[i] == p[j + 1]) j++;
    ne[i] = j;
}

根据上面代码注释中的解释，上述代码等价于：

// 求next数组, ne[1]=0表示如果p[1]没有匹配上，从头开始匹配
for (int i = 2; i <= n; i++) {
    int j = ne[i - 1];
    while (j && p[i] != p[j + 1]) j = ne[j];
    if (p[i] == p[j + 1]) j++;
    ne[i] = j;
}

因此上述代码就可以理解为，根据ne[0]~ne[i-1]求解ne[i]。

• 对应到AC自动机中，KMP中的模式串p需要变为一个trie树，我们其实也可以将KMP中的模式串p看成trie树，只不过这棵树是一个单链而已。我们需要在trie树中求解next数组。

• 类似于KMP中的next数组定义（next[j]=k表示后缀等于非平凡前缀的最大长度对应的下标），AC自动机中next数组定义：next[x]中存储的是trie中的某个节点y，节点y满足从根节点到y代表的字符串等于以节点x为结尾的等长的字符串，且该字符串是非平凡中最长的一个。

• 下面以she、he、say、shr、her这5个单词为例，讲解一下next数组的求解过程：

（1）首先要建立trie树，如下图（假设代表单词的5个节点编号为1~5，实际trie树中不是1~5，这里为了讲解方便）：

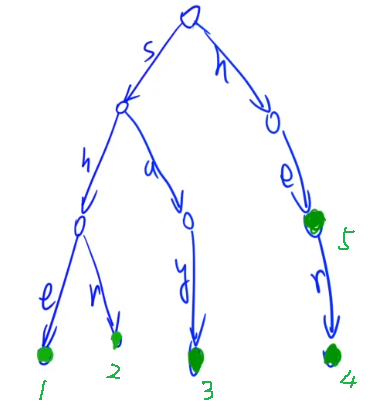
根据定义可知，上图中节点1对应的next值为5，即next[1]=5。

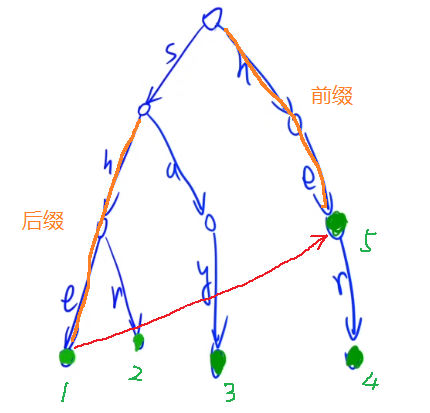
（2）类似于kmp中next[0]=next[1]=0，这里trie树中的第一层和第二层节点的next值也都为0，最终建立出来的trie树如下图：

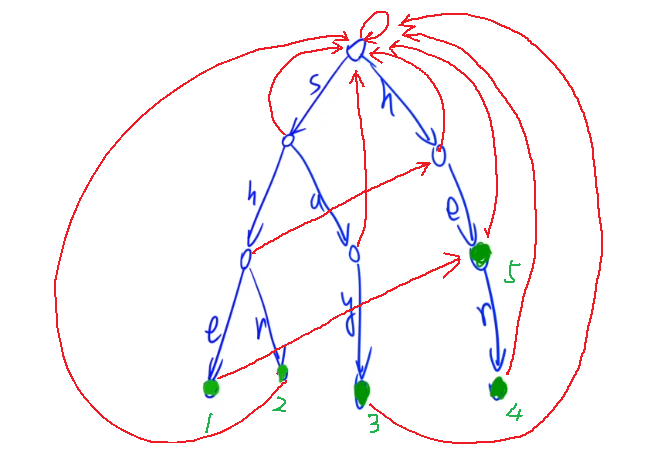
• 对应到代码上，类似于KMP算法根据ne[0]~ne[i-1]求解ne[i]，我们可以在这棵树上做BFS，根据前i-1层的结果来求解第i层的结果。

while (hh <= tt)
{
    int t = q[hh ++ ];
    for (int i = 0; i < 26; i ++ )  // 这里的i枚举的是字母
    {
        int c = tr[t][i];  // 字母i(0代表'a')对应的节点编号为c
        if (!c) continue;  // 说明从节点t不能走到字母i

        int j = next[t];
        while (j && !tr[j][i]) j = next[j];  // !tr[j][i]代表不能从节点j到达字母i
        if (tr[j][i]) j = tr[j][i];  // 如果能达到，更新节点j对应的编号
        next[c] = j;
        q[++tt] = c;
    }
}

代码对应的图示如下：

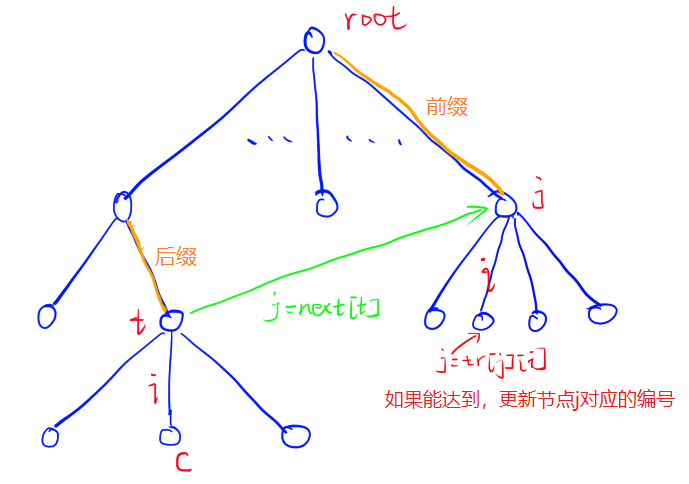
• 匹配过程类似于这里next的求解过程，这里省略。

• AC自动机的时间复杂度也是线性的。

• 对AC自动机进行优化，可以得到trie图。思路是想要将最内层的while循环替换掉，优化一下常数。思想是非类似于路径压缩，因为while循环可能向上跳很多次，我们可以让它跳的时候一步到位，如下图：

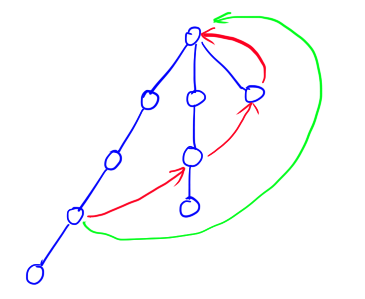
// 此时，tr的定义被更新了，如果有i这个儿子，向下跳；否则不存在这个孩子，直接跳到next指针应该走到的位置
while (hh <= tt)
{
    int t = q[hh ++ ];
    for (int i = 0; i < 26; i ++ )  // 这里的i枚举的是字母
    {
        int &p = tr[t][i];  // 字母i(0代表'a')对应的节点编号为c

        // 如果不存在到i的边，让节点p指向其父节点t的next指向的位置的第i个儿子
        // 即此时tr[t][i]存储了next数组应该存储的内容
        if (!p) p = tr[next[t]][i];
        else {
            next[p] = tr[next[t]][i];
            q[++tt] = p;
        }
    }
}

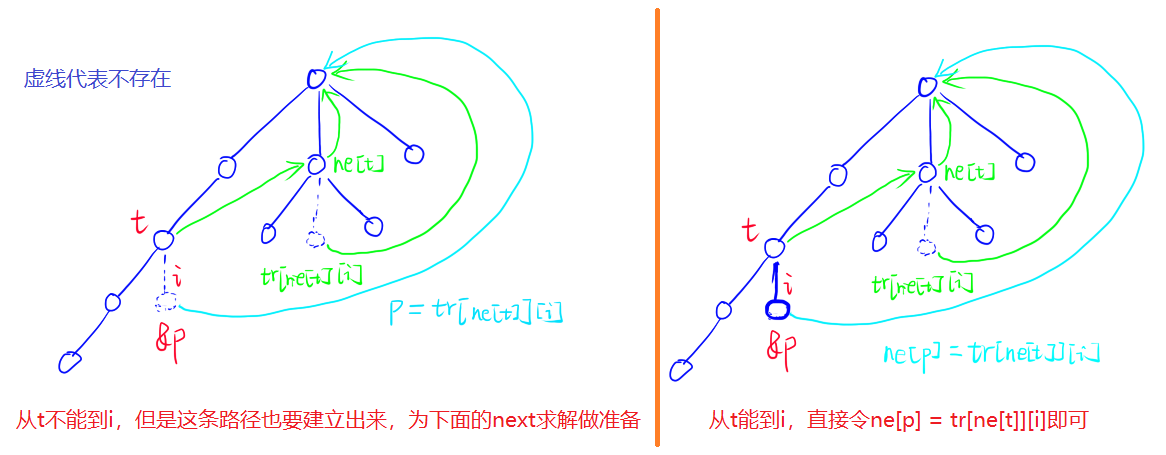
代码

#include <iostream>
#include <cstring>

using namespace std;

const int N = 10010, S = 55, M = 1000010;

int n;  // 单词数量
int tr[N * S][26];
int cnt[N * S];  // 以每个节点结尾的单词的数量
int idx;
char str[M];  // 读取输入字符串
int q[N * S];  // BFS求ne数组时的队列
int ne[N * S];

// trie中的插入函数
void insert() {

    int p = 0;  // 0既代表根节点，也代表空节点
    for (int i = 0; str[i]; i++) {
        int t = str[i] - 'a';
        if (!tr[p][t]) tr[p][t] = ++idx;
        p = tr[p][t];
    }
    cnt[p]++;
}

void build() {

    int hh = 0, tt = -1;
    // 第一层、第二层对应的ne值都为0，直接将第二层入队即可
    for (int i = 0; i < 26; i++)
        if (tr[0][i])  // 根节点0存在孩子i
            q[++tt] = tr[0][i];

    while (hh <= tt) {
        int t = q[hh++];
        for (int i = 0; i < 26; i++) {
            int c = tr[t][i];
            if (!c) continue;

            int j = ne[t];
            while (j && !tr[j][i]) j = ne[j];
            if (tr[j][i]) j = tr[j][i];
            ne[c] = j;
            q[++tt] = c;
        }
    }
}

int main() {

    int T;
    scanf("%d", &T);
    while (T--) {
        memset(tr, 0, sizeof tr);
        memset(cnt, 0, sizeof cnt);
        memset(ne, 0, sizeof ne);
        idx = 0;

        // (1) 建立trie数
        scanf("%d", &n);
        for (int i = 0; i < n; i++) {
            scanf("%s", str);
            insert();
        }

        // (2) 在trie树上求解next数组
        build();

        // (3) 匹配过程：trie树中的单词匹配文章
        scanf("%s", str);
        int res = 0;  // 表示匹配的单词的数量
        for (int i = 0, j = 0; str[i]; i++) {  // 遍历文章中的每个字符
            int t = str[i] - 'a';
            while (j && !tr[j][t]) j = ne[j];
            if (tr[j][t]) j = tr[j][t];

            int p = j;
            while (p) {
                res += cnt[p];
                cnt[p] = 0;  // 该单词如果出现过，统计一遍即可
                p = ne[p];
            }
        }

        printf("%d\n", res);
    }

    return 0;
}

#include <iostream>
#include <cstring>

using namespace std;

const int N = 10010, S = 55, M = 1000010;

int n;  // 单词数量
int tr[N * S][26];
int cnt[N * S];  // 以每个节点结尾的单词的数量
int idx;
char str[M];  // 读取输入字符串
int q[N * S];  // BFS求ne数组时的队列
int ne[N * S];

// trie中的插入函数
void insert() {

    int p = 0;  // 0既代表根节点，也代表空节点
    for (int i = 0; str[i]; i++) {
        int t = str[i] - 'a';
        if (!tr[p][t]) tr[p][t] = ++idx;
        p = tr[p][t];
    }
    cnt[p]++;
}

void build() {

    int hh = 0, tt = -1;
    // 第一层、第二层对应的ne值都为0，直接将第二层入队即可
    for (int i = 0; i < 26; i++)
        if (tr[0][i])  // 根节点0存在孩子i
            q[++tt] = tr[0][i];

    while (hh <= tt) {
        int t = q[hh++];
        for (int i = 0; i < 26; i++) {
            int &p = tr[t][i];

            if (!p) p = tr[ne[t]][i];  // 不存在到i的边
            else {
                ne[p] = tr[ne[t]][i];
                q[++tt] = p;
            }
        }
    }
}

int main() {

    int T;
    scanf("%d", &T);
    while (T--) {
        memset(tr, 0, sizeof tr);
        memset(cnt, 0, sizeof cnt);
        memset(ne, 0, sizeof ne);
        idx = 0;

        // (1) 建立trie数
        scanf("%d", &n);
        for (int i = 0; i < n; i++) {
            scanf("%s", str);
            insert();
        }

        // (2) 在trie树上求解next数组
        build();

        // (3) 匹配过程：trie树中的单词匹配文章
        scanf("%s", str);
        int res = 0;  // 表示匹配的单词的数量
        for (int i = 0, j = 0; str[i]; i++) {  // 遍历文章中的每个字符
            int t = str[i] - 'a';
            j = tr[j][t];

            int p = j;
            while (p) {
                res += cnt[p];
                cnt[p] = 0;  // 该单词如果出现过，统计一遍即可
                p = ne[p];
            }
        }

        printf("%d\n", res);
    }

    return 0;
}