步骤
$\qquad$ 1:求出最小生成树的边权和 sum;
$\qquad$ 2:用最小生成的的边建图(建树)
$\qquad$ 3:用每一条非树边，加入树里，此时一定会有一个环，此时删除环中的(小于插入边的)最大边权，判断这个棵树的边权和是否严格大于sum，如果大于，就在这些大于sun的树中求一个最小值

难点在于第三步，如果直接去求的时间复杂度是$n^2$的
可以用求最近公共祖先(lca)的做法去优化
d1[i][j]:表示从i开始向上跳，跳2^j步的上边权最大值
d2[i][j]:表示从i开始向上跳，跳2^j步的上边权第二大值

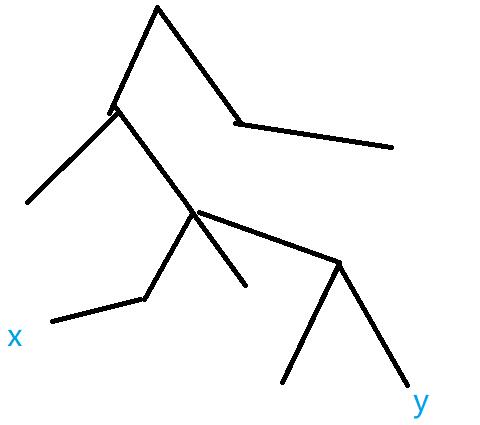
如果我们在x和y的点之间上添加一条边(边权为w)，那么只需要求出(x和y)在跳到他们的最近公共祖先的过程中的所有 最大边权和次大边权。 然后在这些边中去求一个最大值d1，和严格次大值d2。
如果w > d1 此时的生成树的边权和为 sum + s - d1
如果w > d2 此时的生成树的边权和为 sum + s - d2
如果 w <= d2, 这个环类就没有满足要求的答案

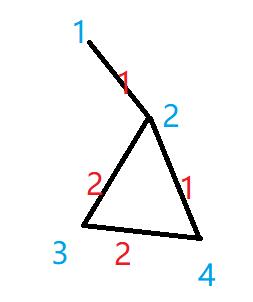
有于我自己也想过是否有可能不需要次大边权，下面这个图就一定是需要次大边权的

#include <cstring>
#include <cstdio>
#include <iostream>
#include <queue>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 100010, M = 300010, INF = 0x3f3f3f3f;

int n, m;
int h[N], e[M], ne[M], w[M], idx;
int p[N];
int depth[N];
int fa[N][17], d1[N][17], d2[N][17];
//d1[i][j]:表示从i开始向上跳，跳2^j步的上边权最大值
struct Edge {
    int a, b, w;
    bool is_uesd;
    bool operator< (const Edge& t) const {
        return w < t.w;
    }
}edge[M];
int q[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

int find(int x)
{
    if(x != p[x]) p[x] = find(p[x]);
    return p[x];
}

LL kruskal()
{
    for(int i = 1;i <= n;i ++) p[i] = i;
    sort(edge, edge + m);

    LL res = 0;
    for(int i = 0;i < m;i ++)
    {
        int a = find(edge[i].a), b = find(edge[i].b), w = edge[i].w;
        if(a != b)
        {
            res += w;
            p[a] = b;
            edge[i].is_uesd = true;
        }
    }
    return res;
}

void build()
{
    memset(h, -1, sizeof h);
    for(int i = 0;i < m;i ++)
        if(edge[i].is_uesd)
        {
            auto [a, b, w, _] = edge[i];
            add(a, b, w), add(b, a, w);
        }
}

void bfs()
{
    memset(depth, 0x3f, sizeof depth);
    depth[0] = 0, depth[1] = 1;
    queue<int> q;
    q.push(1);

    while(q.size())
    {
        int t = q.front();
        q.pop();

        for(int i = h[t]; ~i;i = ne[i])
        {
            int j = e[i];
            if(depth[j] > depth[t] + 1)
            {
                depth[j] = depth[t] + 1;
                q.push(j);

                fa[j][0] = t;
                d1[j][0] = w[i], d2[j][0] = -INF;
                for(int k = 1;k <= 16;k ++)
                {
                    int ancestor = fa[j][k - 1];
                    fa[j][k] = fa[ancestor][k - 1];
                    int distance[4] = {d1[j][k - 1], d2[j][k - 1], d1[ancestor][k - 1], d2[ancestor][k - 1]};
                    d1[j][k] = d2[j][k] = -INF;
                    for(int i = 0;i < 4;i ++)
                    {
                        int d = distance[i];
                        if(d > d1[j][k]) d2[j][k] = d1[j][k], d1[j][k] = d;
                        else if(d != d1[j][k] && d > d2[j][k]) d2[j][k] = d;
                    }
                }
            }
        }
    }
}

int lca(int a, int b, int w)
{
    static int distance[N * 2];
    int cnt = 0;

    if(depth[a] < depth[b]) swap(a, b);
    for(int k = 16;k >= 0;k --)
        if(depth[fa[a][k]] >= depth[b])
        {
            distance[cnt ++] = d1[a][k];
            distance[cnt ++] = d2[a][k];
            a = fa[a][k];
        }
    if(a != b)
    {
        for(int k = 16;k >= 0;k --)
            if(fa[a][k] != fa[b][k])
            {
                distance[cnt ++] = d1[a][k];
                distance[cnt ++] = d2[a][k];
                distance[cnt ++] = d1[b][k];
                distance[cnt ++] = d2[b][k];
                a = fa[a][k];
                b = fa[b][k];
            }

        distance[cnt ++] = d1[a][0];
        distance[cnt ++] = d1[b][0];
    }

    int dist1 = -INF, dist2 = -INF;
    for(int i = 0;i < cnt;i ++)
    {
        int d = distance[i];
        if(d > dist1) dist2 = dist1, dist1 = d;
        else if(d != dist1 && d > dist2) dist2 = d;
    }
    if(w > dist1) return w - dist1;
    if(w > dist2) return w - dist2;
    return INF;
}

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 0;i < m;i ++)
    {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        edge[i] = {a, b, w};
    }

    LL sum = kruskal();
    build();
    bfs();

    LL res = 1e18;
    for(int i = 0;i < m;i ++)
        if(!edge[i].is_uesd)
        {
            auto [a, b, w, _] = edge[i];
            res = min(res, sum + lca(a, b, w));
        }

    printf("%lld\n", res);

    return 0;
}