完全背包

再看完全背包之前推荐先看一下01背包因为有很多共同知识。

完全背包：

每个物品有无限表，表示每新增一个物品可以选取无限次。

思维导图

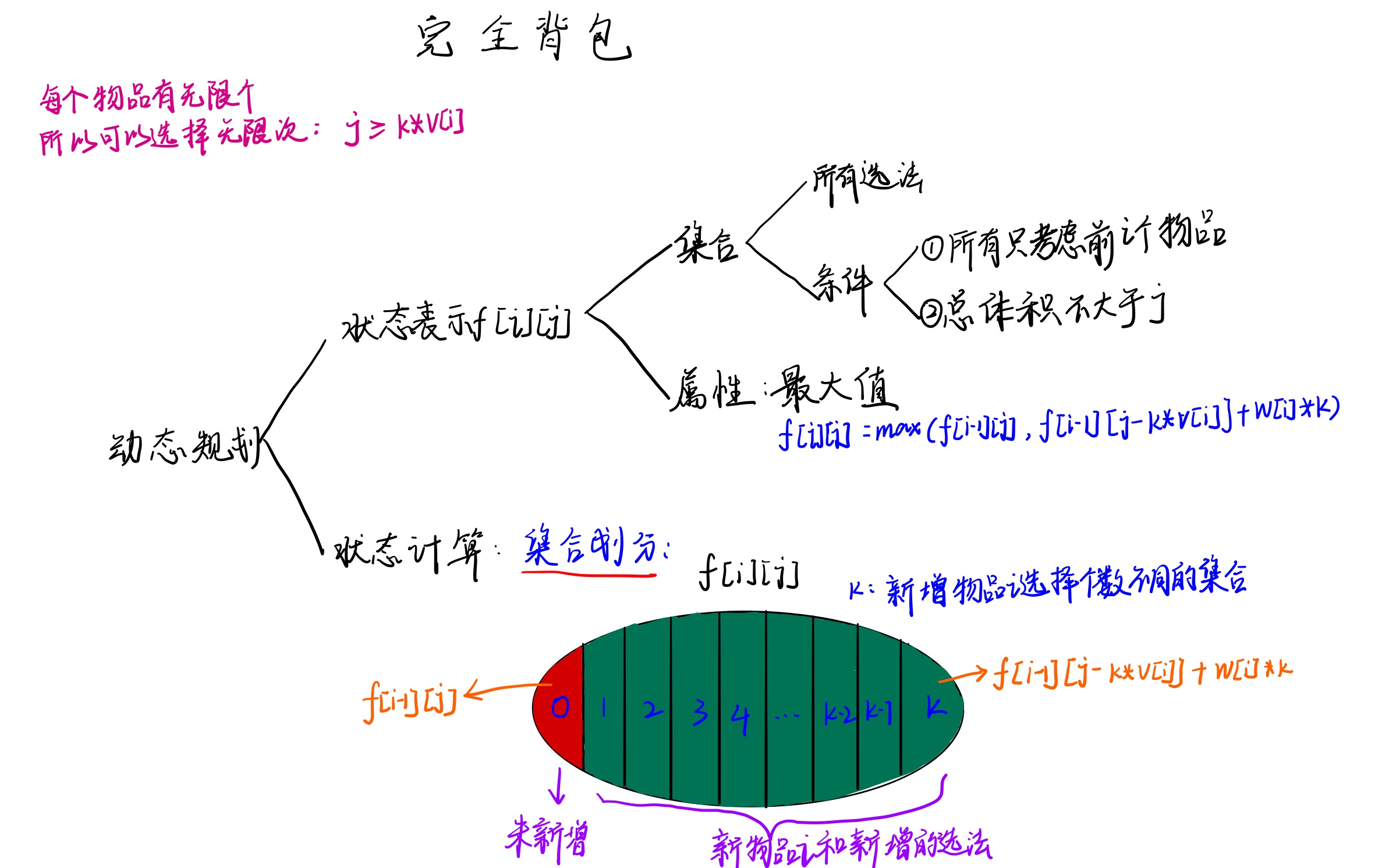
完全背包跟01背包的区别：

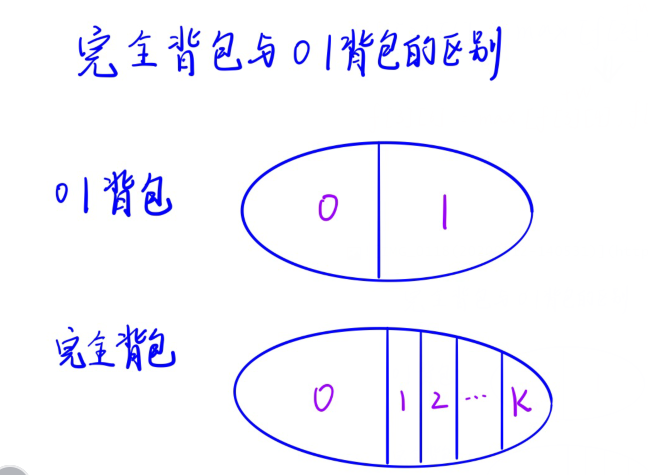
解题步骤：

• 将集合划分成两部分：
• 未包含新增物品i 之前原本的集合 （已知f[i-1][j]）
• 新增物品i 后产生的集合（新增，未知）
• 求集合的最大值的方式相同：分别求出两部分集合的最大值，再求这两个最大值的最大值
• 求新增的集合最大值的方式：对背包容量进行划分
• 第一部分：划分出所有选法中共同拥有的物品（新增物品i）
• 第二部分：剩下的都是不一样的物品
• 新增集合的最大值 = 第一部分的最大值 + 第二部分的最大值

注意：

• 01背包的新增部分只有一个集合
  完全背包的新增部分将其分成多个子集
• 完全背包求新增部分的集合的最大值
• 先求出各个子集的最大值
  • 对背包容量进行划分（跟求新增子集的方法一样）
• 取各个子集最大值的最大值

代码朴素版：

#include<iostream>

using namespace std;
const int N = 1010;

int v[N],w[N];
int f[N][N];

int main()
{
    int n,m;
    cin>>n>>m;
    for(int i = 1; i  <= n; i++)cin>>v[i]>>w[i];

    for(int i = 1; i <= n; i++)
        for(int j = 0; j <= m; j++)
            // 用一个循环对比所有可能子集的最大值
            for(int k = 0; j >= k*v[i]; k++)
                f[i][j] = max(f[i][j],f[i-1][j - k*v[i]] + k * w[i]);
    cout<<f[n][m]<<endl;
    return 0;
}

图解过程 + 初步优化

由下图，我们可以发现很多对比都是重复的，那么我们可以使用前面对比过的结果简化我们的过程

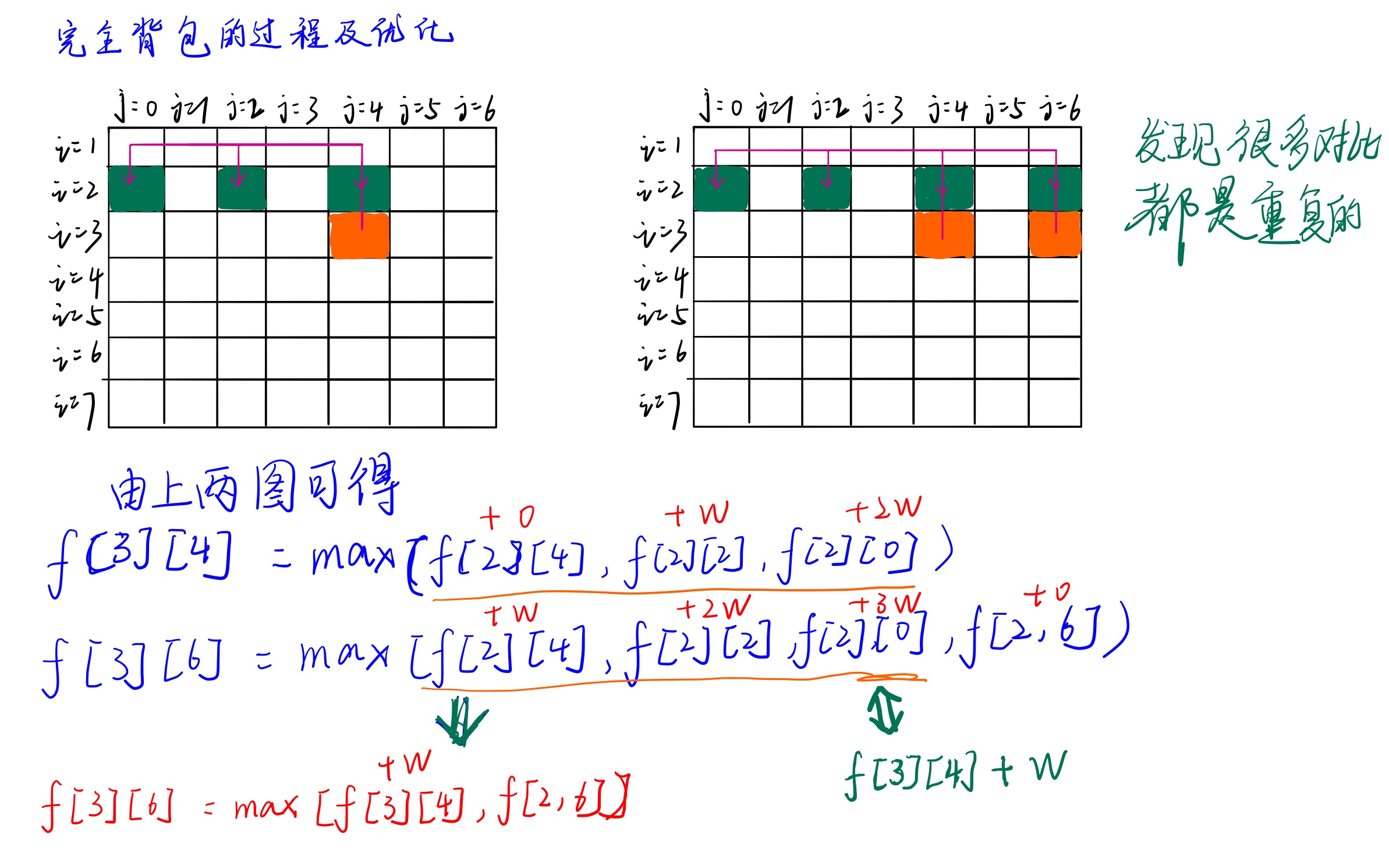
代码初步优化版

#include<iostream>

using namespace std;
const int N = 1010;

int v[N],w[N];
int f[N][N];

int main()
{
    int n,m;
    cin>>n>>m;
    for(int i = 1; i  <= n; i++)cin>>v[i]>>w[i];

    for(int i = 1; i <= n; i++)
        for(int j = 0; j <= m; j++)
            {
                f[i][j]= f[i-1][j];
                if( j >= v[i])
                f[i][j] = max(f[i][j],f[i][j -v[i]] + w[i]);
            }

    cout<<f[n][m]<<endl;
    return 0;
}

优化：二维变一维

通过观察容易得到，我们需要使用到的只是新增物品的前一层的结果就行了，更前面的数据不需要用到。

所以可以使用滚动数组，将二维转化为一维的。

如果所示，完全背包 没有 01背包的那种问题，

因为经过初步优化，跟上一层的多次对比可以简化成跟新更新数据的一次对比，所以完全背包需要对比的是已经更新过的数据，所以遍历的时候只要保证： j >= v[i] * k 就行了并不需要保证对比的是上一层这个问题。

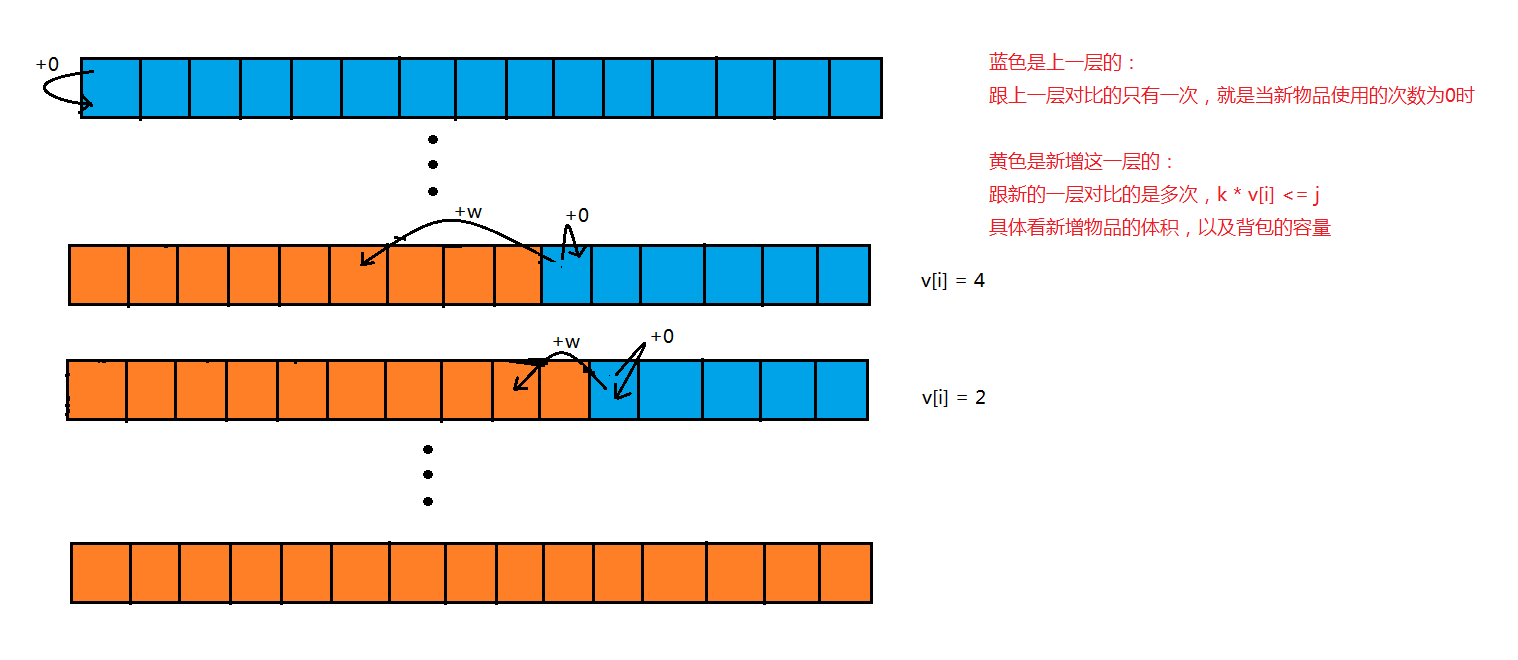
代码终极优化版

#include<iostream>

using namespace std;

const int N = 1010;

int v[N],w[N];
int f[N];

int main()
{
    int n,m;
    cin>>n>>m;

    for(int i = 1; i <= n; i++)cin>>v[i]>>w[i];

    for(int i = 1; i <= n; i++)
        for(int j = v[i]; j <= m; j++)
            // f[j] 表示的是i-1层，f[j-v[i]]表示的是i层
            f[j] = max(f[j],f[j - v[i]] + w[i]);

    cout<<f[m]<<endl;
    return 0;
}