分析

• 平衡树的种类：AVL、RBTree、Splay、Treap、sbt、......

• Treap=Tree(BST) + Heap

• 首先来看什么是BST：Binary Search Tree，即二分搜索树。其定义是递归定义，对于每一个点，其权值严格大于其左子树中所有节点的值，严格小于其右子树所有节点的的值。

• BST有一个很重要的性质：其中序遍历的结果一定是从小到大的序列。

• BST的本质：动态维护一个有序序列（集合）。

• 这里实现的BST，默认BST中每个节点中的值不相同，如果存在多个数据相同的话，可以在每个节点上新开一个变量cnt，用来记录每个数据出现的次数。

• BST中存在的操作：

（1）插入；根据待插入的值的大小递归插入即可。

（2）删除；删除叶节点很容易，如果不是的话可以转化为删除叶节点（针对Treap、Splay都可以转换）。

（3）找前驱/后继；对于任意二叉树，都存在前驱和后继的概念，都与某个二叉树中的节点，其前驱和后继分别是二叉树中序遍历后该节点的前一个数和后一个数。

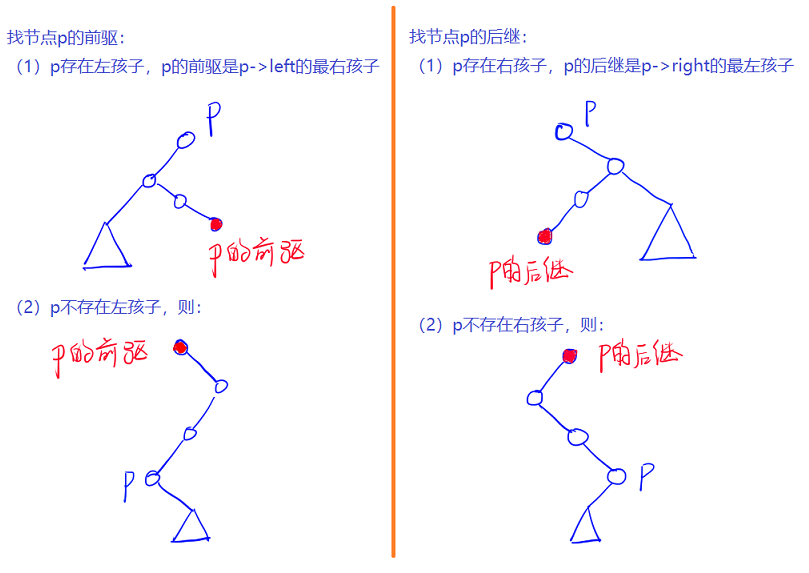
（4）找最大值/最小值；最大值一直沿着右子树遍历即可，最小值一直沿着左子树遍历即可。

（5）求某个值的排名；

（6）求排名是k的数是哪个；

（7）求比某个数x小的最大值；注意：数x不一定在树中出现。

（8）求比某个数x大的最小值；注意：数x不一定在树中出现。

• 一般来说，最大值不存在后继，最小值不存在前驱，为了不用特殊处理这两种情况，我们可以在刚开始建立空BST时就插入两个哨兵，一个负无穷，一个正无穷。

• 可以证明，在随机向BST插入的情况下，其高度是在$log(n)$量级的。基于这个思想，我们希望我们的BST越随机越好，因此引入Treap。

• Treap是一棵BST，同时也是一个堆（这里以大根堆为例），其每个节点的定义如下：

struct Node {
    int l, r;  // 左右孩子的编号
    int key;  // BST中用于排序的值
    int val;  // 堆中需要进行比较的值，是随机生成的
} tr[N];

• 需要说明的一点，如果一棵树中所有的节点的key、val都不相同，则这棵二叉树是唯一确定的。树的根节点是val值最大的节点，比该节点key小的节点都在其左子树中，比该节点key大的节点都在其右子树中，如此下去是一个确定的过程，因此二叉树是唯一的。

• 当存在相同值是，该二叉树不唯一，因为val是随机生成的，因此平均来看，Treap的高度是在$log(n)$量级的。

• 下面介绍平衡树中非常重要的操作：左旋（zag）、右旋（zig），如下图：

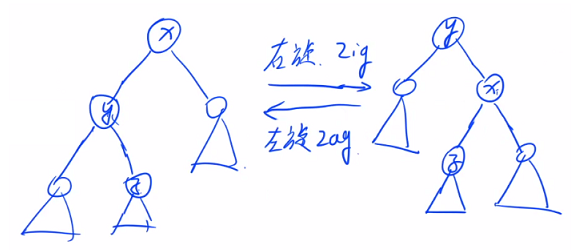
在BST中，左旋和右旋之后整棵树仍然还是BST，即中序遍历还是升序的。

• 在Treap中，每次插入数据时，按照key的大小插入到叶节点中，然后根据随机分配的val将该节点进行上移（shiftUp），即和父节点交换。

• 在Treap中，每次删除一个数据时，假设其左子树权值为val1，右子树权值为val2，如果val1>val2，或者右子树不存在，右旋；否则左旋，则需要被删除的节点高度降低1，直至需要被删除的节点为叶节点，则删除之即可。

// 本题中排名都是指从小到大的排名
#include <iostream>

using namespace std;

const int N = 100010, INF = 1e8;

int n;  // 输入数据个数
struct Node {
    int l, r;  // 左右孩子的编号
    int key;  // BST中用于排序的值
    int val;  // 堆中需要进行比较的值，是随机生成的
    int cnt;  // 值为key的数的数量
    int sz;  // 以当前节点为根节点的子树中数据的总数量(包含自己)
} tr[N];

int root, idx;  // 根节点、每个节点分配的编号

// 根据p的左右孩子计算p
void pushup(int p) {
    tr[p].sz = tr[tr[p].l].sz + tr[tr[p].r].sz + tr[p].cnt;
}

// 新生成一个节点, 返回节点编号
int get_node(int key) {

    tr[++idx].key = key;
    tr[idx].val = rand();
    tr[idx].cnt = tr[idx].sz = 1;
    return idx;
}

// 右旋
void zig(int &p) {  // 这里必须传递引用, 因为插入和删除时传入的root可能发生变化
    /*
        对节点p进行向右旋转操作，返回旋转后新的根节点q
               p                              q
              / \                           /   \
             q   T4     向右旋转 (p)       z     p
            / \       - - - - - - - ->    / \   / \
           z   T3                       T1  T2 T3 T4
          / \
        T1   T2
    */
    int q = tr[p].l;
    tr[p].l = tr[q].r, tr[q].r = p, p = q;  // 此时根节点p变为了q
    pushup(tr[p].r), pushup(p);
}

// 左旋
void zag(int &p) {  // 这里必须传递引用, 因为插入和删除时传入的root可能发生变化
    /*
        对节点p进行向左旋转操作，返回旋转后新的根节点q
           p                             q
         /  \                          /   \
        T1   q      向左旋转 (p)      p     z
            / \   - - - - - - - ->   / \   / \
          T2  z                     T1 T2 T3 T4
             / \
            T3 T4
    */
    int q = tr[p].r;
    tr[p].r = tr[q].l, tr[q].l = p, p = q;  // 此时根节点p变为了q
    pushup(tr[p].l), pushup(p);
}

// 创建Treap
void build() {

    get_node(-INF), get_node(INF);
    root = 1, tr[1].r = 2;  // 设置两个哨兵
    pushup(root);

    if (tr[1].val < tr[2].val) zag(root);
}

// 在以tr[p]为根的树中插入key
void insert(int &p, int key) {

    if (!p) p = get_node(key);
    else if (tr[p].key == key) tr[p].cnt++;
    else if (tr[p].key > key) {  // key应该插到左子树中
        insert(tr[p].l, key);
        if (tr[tr[p].l].val > tr[p].val) zig(p);
    } else {
        insert(tr[p].r, key);
        if (tr[tr[p].r].val > tr[p].val) zag(p);
    }
    pushup(p);  // 需要更新当前节点的sz
}

void remove(int &p, int key) {

    if (!p) return;  // 删除的节点不存在
    if (tr[p].key == key) {
        if (tr[p].cnt > 1) tr[p].cnt--;
        else if (tr[p].l || tr[p].r) {  // 至少存在一棵子树
            if (!tr[p].r || (tr[p].l && tr[tr[p].l].val > tr[tr[p].r].val)) {
                zig(p);
                remove(tr[p].r, key);
            } else {  // 说明右子树不为空
                zag(p);
                remove(tr[p].l, key);
            }
        } else p = 0;  // 说明p是叶节点且tr[p].cnt == 1, 可以直接删除
    } else if (tr[p].key > key) remove(tr[p].l, key);
    else remove(tr[p].r, key);

    pushup(p);
}

// 通过数值找排名
int get_rank_by_key(int p, int key) {

    if (!p) return 0;  // 本题中不会发生此情况
    if (tr[p].key == key) return tr[tr[p].l].sz + 1;
    if (tr[p].key > key) return get_rank_by_key(tr[p].l, key);
    // 否则应该到p的右子树中找key，其排名是左子树节点个数+p.cnt+右子树排名
    return tr[tr[p].l].sz + tr[p].cnt + get_rank_by_key(tr[p].r, key);
}

// 通过排名找数值
int get_key_by_rank(int p, int rank) {

    if (!p) return INF;  // 本题中不会发生此情况
    if (tr[tr[p].l].sz >= rank) return get_key_by_rank(tr[p].l, rank);
    // 否则说明tr[tr[p].l].sz < rank
    if (tr[tr[p].l].sz + tr[p].cnt >= rank) return tr[p].key;
    // 否则说明tr[tr[p].l].sz + tr[p].cnt < rank
    return get_key_by_rank(tr[p].r, rank - tr[tr[p].l].sz - tr[p].cnt);
}

// 找到严格小于key的最大数
int get_prev(int p, int key) {

    if (!p) return -INF;
    if (tr[p].key >= key) return get_prev(tr[p].l, key);
    return max(tr[p].key, get_prev(tr[p].r, key));
}

// 找到严格大于key的最小数
int get_next(int p, int key) {

    if (!p) return INF;
    if (tr[p].key <= key) return get_next(tr[p].r, key);
    return min(tr[p].key, get_next(tr[p].l, key));
}

int main() {

    build();

    scanf("%d", &n);
    while (n--) {
        int opt, x;
        scanf("%d%d", &opt, &x);
        if (opt == 1) insert(root, x);
        else if (opt == 2) remove(root, x);
        else if (opt == 3) printf("%d\n", get_rank_by_key(root, x) - 1);  // 考虑哨兵
        else if (opt == 4) printf("%d\n", get_key_by_rank(root, x + 1));  // 考虑哨兵
        else if (opt == 5) printf("%d\n", get_prev(root, x));
        else printf("%d\n", get_next(root, x));
    }

    return 0;
}