题目描述

对于一个字符串$S$，我们定义$S$的分值$f(S)$为$S$中恰好出现一次的字符个数。

例如 $f(“aba”)=1$，$f(“abc”)=3$, $f(“aaa”)=0$。

现在给定一个字符串 $S[0…n−1]$（长度为 $n$），请你计算对于所有 $S$ 的非空子串 $S[i…j]$($0≤i≤j<n$)， $f(S[i…j]$) 的和是多少。

暴力 $O(n^2)$

过六个点
考虑暴力做法
先枚举每个字符，对于每个字符，向前枚举以当前字符结尾的子串
并计算每个子串的分值是多少
计算每个子串分值过程可以递推，转移的过程$O(1)$
求出以当前字符结尾所有子串的分值时间复杂度$O(n)$
最后累加所有分值即可。
总的时间复杂度$O(n^2)$

C++ 代码实现

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;

const int N = 1e5 + 10;
char str[N];
typedef long long LL;
bool st[26];
int main() {
    scanf("%s", str + 1);
    int n = strlen(str + 1);
    LL ans = 0;
    for(int i = 1; i <= n; ++i) {
        memset(st, 0, sizeof st);
        int t = str[i] - 'a';
        st[t] = true;
        int cnt = 1;
        ans += cnt;
        for(int j = i - 1; j >= 1; --j) {
            int t = str[j] - 'a';        
            if(!st[t]) {//未出现过该字符, 分数+1
                cnt++;
                st[t] = true;
            }
            ans += cnt;
        }
    }

    printf("%lld\n", ans);
    return 0;
}

DP $O(n)$

$AC$
下面对暴力做法进行优化
首先考虑暴力做法时间复杂度的瓶颈$ –> $求解以当前字符结尾所有子串的分值
那么，就设$f[i]$表示以$str[i]$为结尾的所有子串的总分值
如果能够找到$f[i]$和$f[i-1]$之间的关系，则可以递推求解。
通过下标对整个集合进行划分

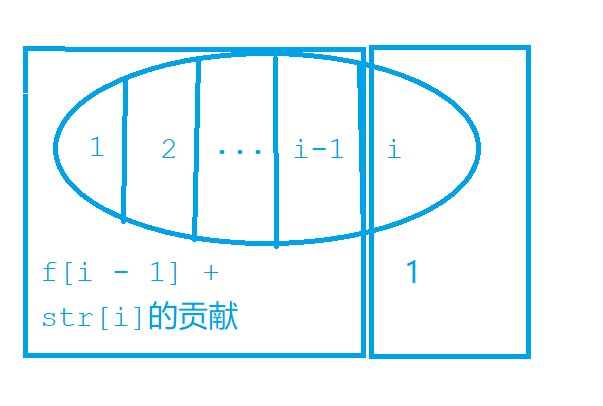
而第$i$个新增元素$str[i]$定会有子集$str[i]$, 故产生贡献值为1
则问题转化为求解加入一个字符$str[i]$后对前面$i-1$个子串产生的影响，即可以看成是$str[i]$的贡献值
由于$str[i]$可以影响到它前面连续的不等同于$str[i]$的串的分值，并且每个子串的分值至多$+1$
故可以通过记录每个字符最后出现的位置$pos$
则多出$str[i]$后比$f[i - 1]$多产生的分数就是$i - 1 - pos$
故$f[i] = f[i - 1] + i - pos$

遍历字符串$O(n)$, 状态转移$O(1)$, 总的时间复杂度$O(n)$

C++ 代码实现

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;

const int N = 1e5 + 10;
char str[N];
typedef long long LL;
int pos[26];//记录每个字符最后一次出现的位置
int f[N];
int main() {
    scanf("%s", str + 1);
    int n = strlen(str + 1);
    LL ans = 0;
    for(int i = 1; i <= n; ++i) {
        int t = str[i] - 'a';
        f[i] = f[i - 1] + i - pos[t];
        pos[t] = i;
        ans += f[i];
    }

    printf("%lld\n", ans);
    return 0;
}