F: 特别数的和
小明对数位中含有 2、0、1、9 的数字很感兴趣(不包括前导 0),在 1 到40 中这样的数包括 1、2、9、10 至 32、39 和 40,共 28 个,他们的和是 574。
请问,在 1 到 n 中,所有这样的数的和是多少?
样例
输入
40
输出
574
数据范围
对于$ 20% $的评测用例,$1 ≤ n ≤ 10$。
对于 $50%$ 的评测用例,$1 ≤ n ≤ 100$。
对于 $80%$ 的评测用例,$1 ≤ n ≤ 1000$。
对于所有评测用例,$1 ≤ n ≤ 10000$。
C++ 代码
#include<iostream>
using namespace std;
int main(){
int res=0,n;
cin>>n;
for(int i=1;i<=n;i++){
int a=i,b;
while(a!=0){
b=a%10;
if(b==2||b==0||b==1||b==9){
res+=i;
break;
}
a/=10;
}
}
cout<<res<<endl;
}
G: 完全二叉树的权值
给定一棵包含 N 个节点的完全二叉树,树上每个节点都有一个权值,按从上到下、从左到右的顺序依次是 $A_1, A_2, · · · A_N$,如下图所示:
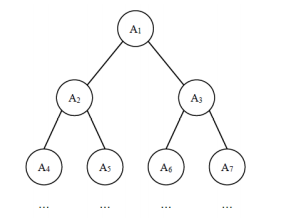
现在小明要把相同深度的节点的权值加在一起,他想知道哪个深度的节点权值之和最大?
如果有多个深度的权值和同为最大,请你输出其中最小的深度。
注:根的深度是 1。
样例
输入
第一行包含一个整数 N。
第二行包含 N 个整数$ A_1, A_2, · · · A_N$ 。
7
1 6 5 4 3 2 1
输出
2
数据范围
对于所有评测用例,$1 ≤ N ≤ 100000,−100000 ≤ Ai ≤ 100000$。
思路
主要是满二叉树的特性
需要计算每一层的权值和,权值和最大值,权值和最大的层次,当前层次,当前层最多结点数。
要注意数据范围,以及正负的问题
C++ 代码
#include <bits/stdc++.h>
using namespace std;
int main(){
int n;
int leaves=1;
int flo=1;
int result;
long int temp=-1000000;
scanf("%d",&n);
while(n){
long int count=0;
int number;
for(int i=0;i<leaves;i++){
scanf("%d",&number);
n--;
count+=number;
if(n==0) break;
}
if(count>temp){
temp=count;
result=flo;
}
flo++;
leaves*=2;
}
cout<<result<<endl;
return 0;
}
H: 等差数列
数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了一部分的数列,只记得其中 N 个整数。
现在给出这 N 个整数,小明想知道包含这 N 个整数的最短的等差数列有几项?
样例
输入的第一行包含一个整数 N。
第二行包含 N 个整数 $A_1, A_2, · · · , A_N$。(注意 $A_1 ∼ A_N$ 并不一定是按等差数列中的顺序给出)
输入:
5
2 6 4 10 20
输出
10
数据范围
对于所有评测用例,$2 ≤ N ≤ 100000,0 ≤ A_i ≤ 10_9$。
$A_i$的范围在int内,所以开int就可以
思路
对数据排序后,求差值,之后求差值最大公约数,即是公差。
⭐
会有常数数列的可能,在做除法的时候一定要注意分母会不会为0
最大公约数可以自己敲模板,也可以直接调用函数__gcd(int a,int b)
C++ 代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e5;
int e[N],d[N];
int gcd(int a,int b){
if(b) return gcd(b,a%b);
return a;
}
int main(){
int n;
cin>>n;
for(int i=0;i<n;i++){
cin>>e[i];
}
sort(e,e+n);
for(int i=1;i<n;i++){
d[i]=e[i]-e[i-1];
}
int t=d[1],res=0;
for(int i=2;i<n;i++){
t=gcd(t,d[i]);
}
if(t==0){
cout<<n<<endl;
return 0;
}
for(int i=1;i<n;i++){
res+=d[i]/t-1;
}
cout<<res+n<<endl;
}
I: 后缀表达式
给定 N 个加号、M 个减号以及 N + M + 1 个整数$ A_1, A_2, · · · , A_{N+M+1}$,小
明想知道在所有由这 N 个加号、M 个减号以及 N + M + 1 个整数凑出的合法的后缀表达式中,结果最大的是哪一个?
请你输出这个最大的结果。
例如使用1 2 3 + -,则 “2 3 + 1 -” 这个后缀表达式结果是 4,是最大的。
样例
输入
第一行包含两个整数 N 和 M。
第二行包含 N + M + 1 个整数$ A_1, A_2, · · · , A_{N+M+1}$。
1 1
1 2 3
输出
4
数据范围
对于所有评测用例,$0 ≤ N, M ≤ 100000,−10_9 ≤ Ai ≤ 10_9$
思路
C++ 代码
J: 灵能传输
你控制着 n 名高阶圣堂武士,方便起见标为$ 1, 2, · · · , n$。每名高阶圣堂武士
需要一定的灵能来战斗,每个人有一个灵能值 $a_i$ 表示其拥有的灵能的多少($a_i$
非负表示这名高阶圣堂武士比在最佳状态下多余了 $a_i$ 点灵能,$a_i$ 为负则表示这
名高阶圣堂武士还需要 $−a_i$ 点灵能才能到达最佳战斗状态)。现在系统赋予了你的高阶圣堂武士一个能力,传递灵能;
每次你可以选择一个 $i ∈ [2, n − 1]$.
若$a_i ≥ 0$ 则其两旁的高阶圣堂武士,也就是 $i − 1$、$i+1$这两名高阶圣堂武士会从i这名高阶圣堂武士这里各抽取 $a_i$ 点灵能;
若 $a_i < 0$ 则其两旁的高阶圣堂武士,也就是 $i − 1$, $i + 1$ 这两名高阶圣堂武士会给 i 这名高阶圣堂武士 $−a_i$ 点灵能。
形式化来讲就是 $a_i−1+ = a_i$, $a_i+1+ = a_i$, $a_i− = 2a_i$。
灵能是非常高效的作战工具,同时也非常危险且不稳定,一位高阶圣堂武士拥有的灵能过多或者过少都不好,定义一组高阶圣堂武士的不稳定度为$max |ai|$,请你通过不限次数的传递灵能操作使得你控制的这一组高阶圣堂武士的不稳定度最小。
样例
数据范围
思路
C++ 代码

