题目描述

有 N 头牛在畜栏中吃草。

每个畜栏在同一时间段只能提供给一头牛吃草，所以可能会需要多个畜栏。

给定 N 头牛和每头牛开始吃草的时间 A 以及结束吃草的时间 B，每头牛在 [A,B] 这一时间段内都会一直吃草。

当两头牛的吃草区间存在交集时（包括端点），这两头牛不能被安排在同一个畜栏吃草。

求需要的最小畜栏数目和每头牛对应的畜栏方案。

输入格式
第 1 行：输入一个整数 N。

第 2..N+1 行：第 i+1 行输入第 i 头牛的开始吃草时间 A 以及结束吃草时间 B，
数之间用空格隔开。

输出格式
第 1 行：输入一个整数，代表所需最小畜栏数。

第 2..N+1 行：第 i+1 行输入第 i 头牛被安排到的畜栏编号，
编号是从 1 开始的 连续 整数，只要方案合法即可。

数据范围
1≤N≤50000,
1≤A,B≤1000000
输入样例：
5
1 10
2 4
3 6
5 8
4 7
输出样例：
4
1
2
3
2
4

算法1

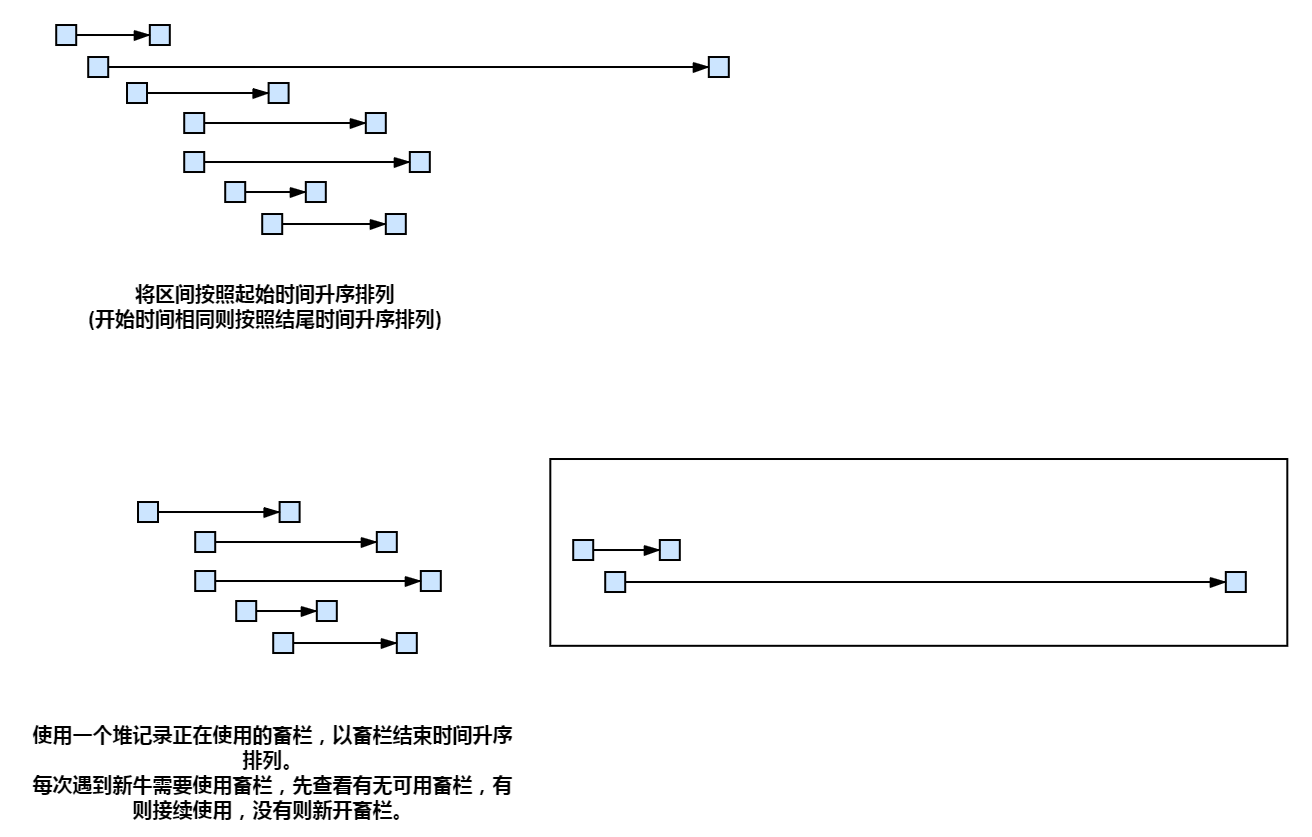
C++ 代码

// 111畜栏预订.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
//

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>

using namespace std;


const int N = 50010;
int n;
int ans[N];

struct COWS {
    int st, ed, num;
}cows[N];

bool cmp(const struct COWS &a, const struct COWS &b) {
    if (a.st < b.st) return true;
    else if (a.st == b.st) return a.ed < b.ed;
    return false;
}

struct QUEUE_CMP {
    bool operator()(const struct COWS &a, const struct COWS &b)
    {
        return a.ed > b.ed;
    }
};


int main()
{
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> cows[i].st >> cows[i].ed;
        cows[i].num = i + 1;
    }

    sort(cows,cows+n,cmp);

    int count = 0;
    priority_queue <struct COWS, vector<struct COWS>, QUEUE_CMP> q;

    for (int i = 0; i < n; i++) {
        if (q.empty() || q.top().ed >= cows[i].st ) {
            //开启新畜栏
            count++;
            ans[cows[i].num] = count;
            q.push(cows[i]);
        }
        else {
            //使用之前的畜栏
            ans[cows[i].num] = ans[q.top().num];
            q.pop();
            q.push(cows[i]);
        }
    }

    cout << count << endl;
    for (int i = 1; i <= n; i++) {
        cout << ans[i] << endl;
    }


    return 0;
}

我的视频题解空间