题目描述

小明正在做一个网络实验。

他设置了 n台电脑，称为节点，用于收发和存储数据。

初始时，所有节点都是独立的，不存在任何连接。

小明可以通过网线将两个节点连接起来，连接后两个节点就可以互相通信了。

两个节点如果存在网线连接，称为相邻。

小明有时会测试当时的网络，他会在某个节点发送一条信息，信息会发送到每个相邻的节点，之后这些节点又会转发到自己相邻的节点，直到所有直接或间接相邻的节点都收到了信息。

所有发送和接收的节点都会将信息存储下来。

一条信息只存储一次。

给出小明连接和测试的过程，请计算出每个节点存储信息的大小。

输入格式
输入的第一行包含两个整数 n,m，分别表示节点数量和操作数量。节点从 1至 n
编号。
接下来 m行，每行三个整数，表示一个操作。
如果操作为 1 a b，表示将节点 a和节点 b，通过网线连接起来。当 a = b 时，表示连接了一个自环，对网络没有实质影响。
如果操作为 2 p t，表示在节点 p上发送一条大小为 t的信息。

输出格式
输出一行，包含 n
个整数，相邻整数之间用一个空格分割，依次表示进行完上述操作后节点 1 至节点 n上存储信息的大小。

数据范围
1≤n≤10000,
1≤m≤105,
1≤t≤100

样例

输入样例1：

4 8
1 1 2
2 1 10
2 3 5
1 4 1
2 2 2
1 1 2
1 2 4
2 2 1

输出样例1：

13 13 5 3


输入样例2：
11 20
2 5 90
2 3 21
2 3 83
1 11 7
1 10 11
1 3 9
1 4 9
1 2 1
1 3 9
2 7 54
1 8 6
1 3 4
2 6 9
1 10 4
1 2 4
1 10 7
1 1 3
1 1 7
2 6 85
2 3 75
输出样例2：
75 75 179 75 90 94 129 94 75 129 129

暴力： (过不了的呢)

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
using namespace std;
int n,m;
int num[100005];
int a,x,y;
int pre[100005];
int Find(int x){
    if(x!=pre[x]) pre[x]=Find(pre[x]);
     return pre[x];
}
void join(int x,int y){
    int a=Find(x);
    int b=Find(y);
    if(a!=b){
        pre[a]=b;
    }
}
int main(int argc, char** argv) {
    for(int i=0;i<100005;i++){
        pre[i]=i;
    }
    scanf("%d%d",&n,&m);
    while(m--){
        scanf("%d%d%d",&a,&x,&y);
        if(a==1){
            join(x,y);
        }else{
            int t=Find(x);
            for(int i=1;i<=n;i++){
                if(t==Find(i)){
                    num[i]+=y;  
                }
            }
        }
    }
    for(int i=1;i<=n;i++){
        printf("%d ",num[i]);
    }
        return 0;
}

正解：（书上差分）：
不理解的话可以根据样例2手动模拟理解一下：

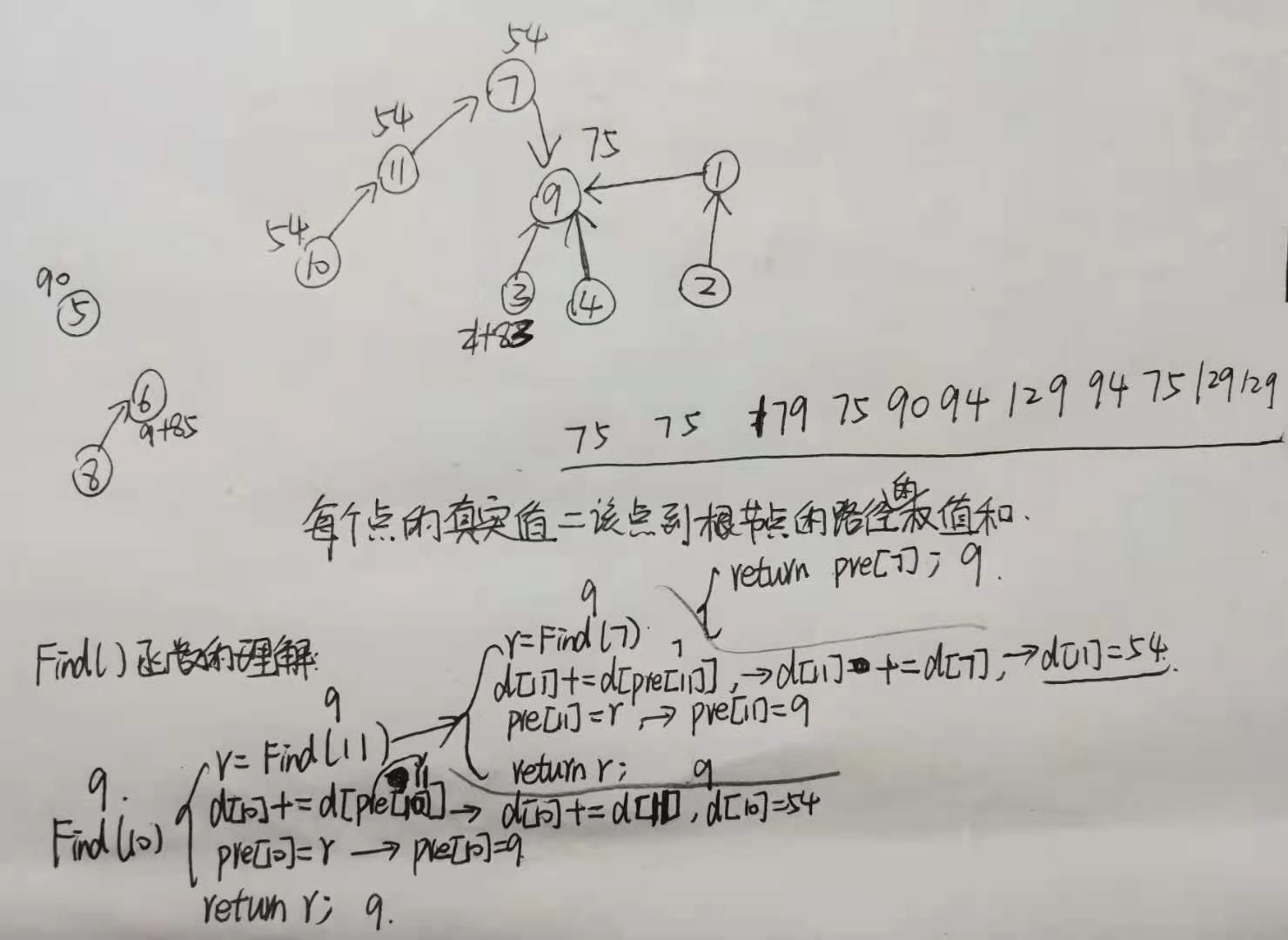
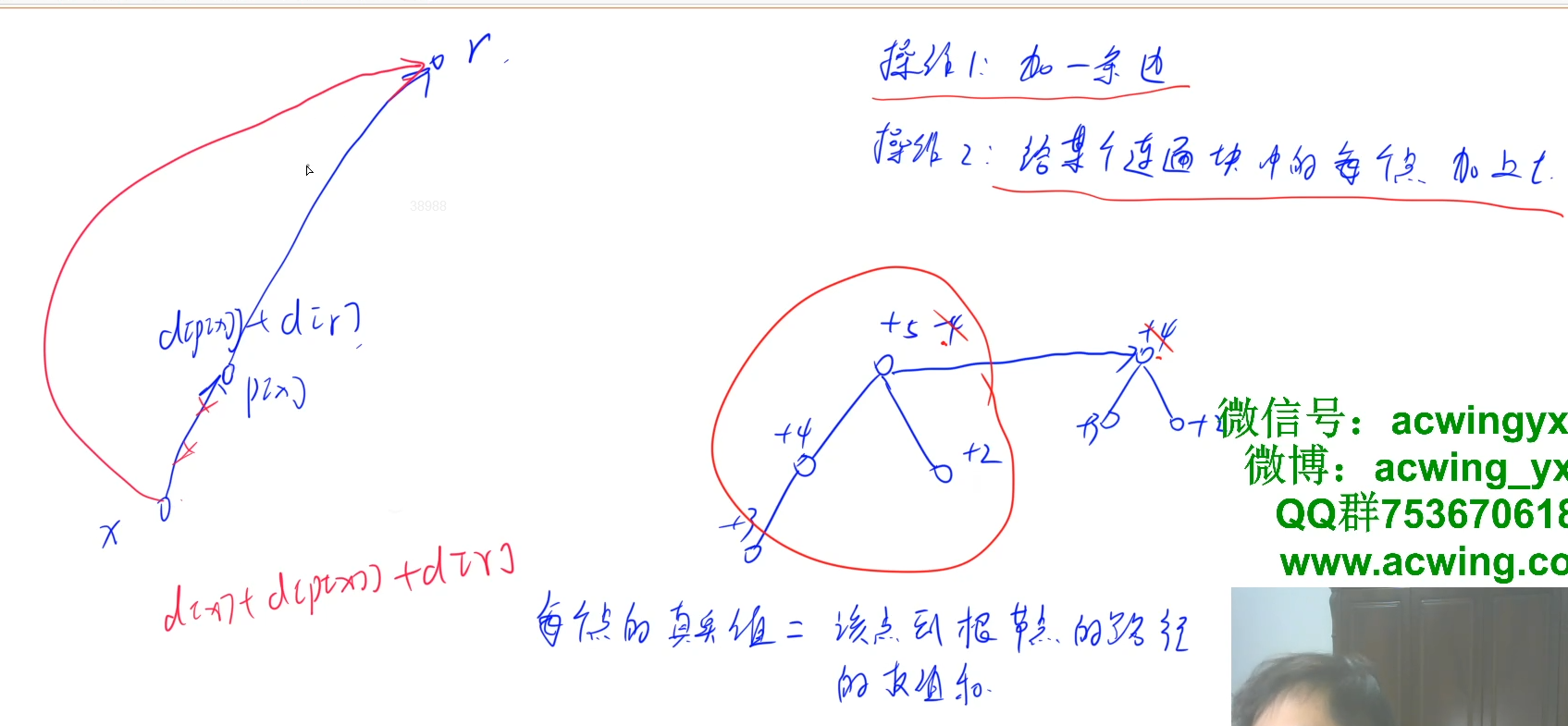
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
using namespace std;
int n,m;
int d[100005];
int a,x,y;
int pre[100005];
int Find(int x){
    if(x==pre[x]||pre[pre[x]]==pre[x]){
        return pre[x];
    }
    int r=Find(pre[x]);//这一步调用的Find函数返回后别忘了执行后面的语句
    d[x]+=d[pre[x]];//看不懂就根据样例2手动模拟一下
    pre[x]=r;//直接赋值pre[x]=根节点，下次再想找x的父节点就不用花大量时间遍历了，pre数组里存的就是
    return r;
}
void join(int x,int y){
    int a=Find(x);
    int b=Find(y);
    if(a!=b){
        d[a]-=d[b];
        pre[a]=b;
    }
}
int main(int argc, char** argv) {
    for(int i=0;i<100005;i++){
        pre[i]=i;
    }
    scanf("%d%d",&n,&m);
    while(m--){
        scanf("%d%d%d",&a,&x,&y);
        if(a==1){
            join(x,y);
        }else{
            x=Find(x);
            d[x]+=y;
        }
    }
    for(int i=1;i<=n;i++){
        if(i==Find(i)){
            printf("%d ",d[i]);//根节点就直接输出权值
        }
        else{//每个节点的权值就等于该点的权值加上根节点的权值
            printf("%d ",d[i]+d[Find(i)]);
        }
    }
    printf("\n");
        return 0;
}