数星星

题目

天空中有一些星星，这些星星都在不同的位置，每个星星有个坐标。

如果一个星星的左下方（包含正左和正下）有 k 颗星星，就说这颗星星是 kk 级的。

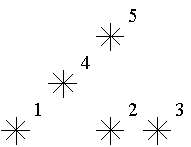
例如，上图中星星 5 是 3 级的（1,2,4 在它左下），星星 2,4 是 1 级的。

例图中有 1 个 0 级，2 个 1 级，1 个 2 级，1 个 3 级的星星。

给定星星的位置，输出各级星星的数目。

换句话说，给定 N 个点，定义每个点的等级是在该点左下方（含正左、正下）的点的数目，试统计每个等级有多少个点。

输入格式

第一行一个整数 N，表示星星的数目；

接下来 N 行给出每颗星星的坐标，坐标用两个整数 x,y 表示；

不会有星星重叠。星星按 y 坐标增序给出，y 坐标相同的按 x 坐标增序给出。

输出格式

N 行，每行一个整数，分别是 0 级，1 级，2 级，……，N−1 级的星星的数目。

数据范围

1 ≤ N ≤ 15000,
0 ≤ x,y ≤ 32000

输入样例：

5
1 1
5 1
7 1
3 3
5 5

输出样例：

1
2
1
1
0

题解

思路

1、y坐标的特殊性

这里因为题目的特殊性，y坐标是不需要进行考虑的。

因为，后面输入的坐标，一定不小于前面的y坐标
$$ y_i <= y_{i+1} $$
正因为如此，只需要考虑横坐标即可。

2、利用x坐标使用树状数组

因为不需要考虑 y坐标 ，因此后面的坐标只需要考虑横坐标即可。

可以使用树状数组进行存储x坐标的信息。进行添加数据，求和等操作。

代码

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;

const int M = 32000 + 10;
int tre[M];
int levs[M]; //树状数组 , 级别数组

//最低位 
int lowbit(int x)
{
    return x & -x;
}

//加上数字
void add(int idx)
{
    for(int i = idx ; i<M ; i+=lowbit(i) ) tre[i]++;
}

//求和
int sum(int idx)
{
    int ans = 0;
    for(int i = idx ; i > 0 ; i -= lowbit(i)) ans += tre[i];
    return ans;
}

int main()
{
    int n;
    scanf("%d",&n);

    for(int i = 0 ; i<n ; i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        x++;//位置从1开始

        //因为题目的特殊性，后面输入的坐标不需要考虑y坐标了，只需要统计x坐标符合的个数

        //更新层级数组个数
        levs[sum(x)]++;

        //添加个数
        add(x);

    }


    //输出层级
    for(int i = 0 ; i<n; i++)
    {
        printf("%d\n",levs[i]);
    }


    return 0;
}