寻找矩阵的极小值（二分）

题目：

给定一个 n×nn×n 的矩阵，矩阵中包含 n×nn×n 个 互不相同 的整数。

定义极小值：如果一个数的值比与它相邻的所有数字的值都小，则这个数值就被称为极小值。

一个数的相邻数字是指其上下左右四个方向相邻的四个数字，另外注意，处于边界或角落的数的相邻数字可能少于四个。

要求在 O(nlogn)O(nlogn) 的时间复杂度之内找出任意一个极小值的位置，并输出它在第几行第几列。

本题中矩阵是隐藏的，你可以通过我们预设的 intint 函数 queryquery 来获得矩阵中某个位置的数值是多少。

例如，query(a,b)query(a,b) 即可获得矩阵中第 aa 行第 bb 列的位置的数值。

注意：

1. 矩阵的行和列均从 00 开始编号。
2. query()函数的调用次数不能超过 (n+2)×⌈log2n⌉+n(n+2)×⌈log2n⌉+n。
3. 答案不唯一，输出任意一个极小值的位置即可。

数据范围

1≤n≤3001≤n≤300，矩阵中的整数在int范围内。

输入样例：

[[1, 2, 3], [4, 5, 6], [7, 8, 9]]

输出样例：

[0, 0]

$$ 要求在时间复杂度为O（nlogn）之内找到极小值 $$

思路：

正常遍历的算法：线性–O（N^2）

三种情况

①：V<L , V<R

②：L<V

③：R<V

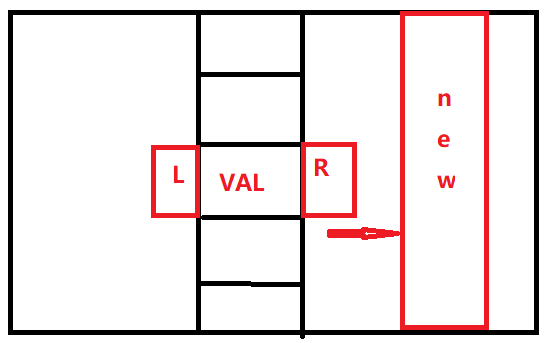
分析：假设遍历一列，找到当前列的极小值VAL，则对其两端进行判断，如果R<Val，从R开始走，则R必定不会寻找返回到当前列，则R去新列寻找，依次循环即可。

二分所有列，N列->最终二分【logn】次（上取整），每一次都需要遍历一整列格子，以及左右（L、R格子）

查询上限：【logn】* (n+2)+n(初始列)

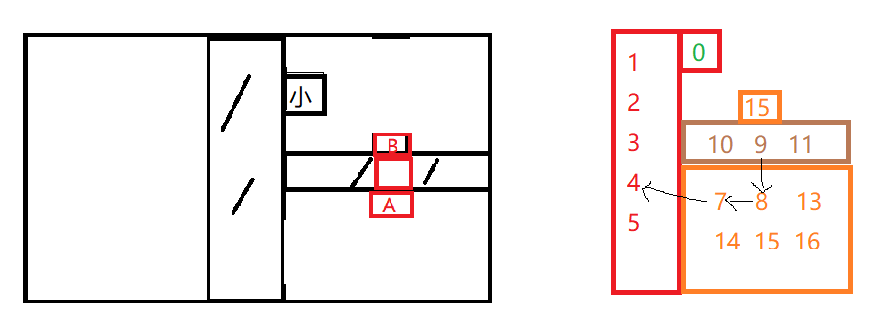
行列二分的错误性：

如果从右边列开始进行二分，如果B[HTML_REMOVED]A时，则从下区间进行二分 ，则有原路返回的可能，与开局结论相悖。

AC代码

// Forward declaration of queryAPI.
// int query(int x, int y);
// return int means matrix[x][y].

class Solution {
public:
    vector<int> getMinimumValue(int n) {
        typedef long long LL;
        const LL INF=1e15;

        int l=0,r=n-1;
        while(l<r){
            //找到最小中间列的位置
            int mid=l+r>>1;

            int k;//记录行的位置
            LL val=INF;
            for(int i=0;i<n;i++){
                int t=query(i,mid);
                //query()接口 ， 返回矩阵一个值
                if(t<val){
                    val=t;
                    k=i;
                }
            }

            //mid>0 求出第k行 mid-1的值
            LL left = mid ? query(k, mid - 1) : INF;
            //如果mid在边界范围内 求出右边的值
            LL right = mid + 1 < n ? query(k, mid + 1) : INF;

            if(val<left&&val<right) return {k,mid};//

            if(left<val){
                //左边一定有解
                r=mid-1;
            }
            //否则右边一定有解
            else l=mid+1;
        }
        //二分后剩下的最后一列
        int k;
        LL val = INF;
        for (int i = 0; i < n; i ++ )
        {
            int t = query(i, r);
            if (t < val)
            {
                val = t;
                k = i;
            }
        }

        return {k,r};
    }
};