树形DP求树的直径
本题有两个难点:
- 树的直径如何求? (树形DP,更新最大值和次大值)
- 如何判断点在直径上? (往下走最大值(已求) + 往上走最大值 == 直径,即在直径上)
- 往上走怎么求? (取决于
u这个点往上走或往下走的最大值(特判往下走不能走回))
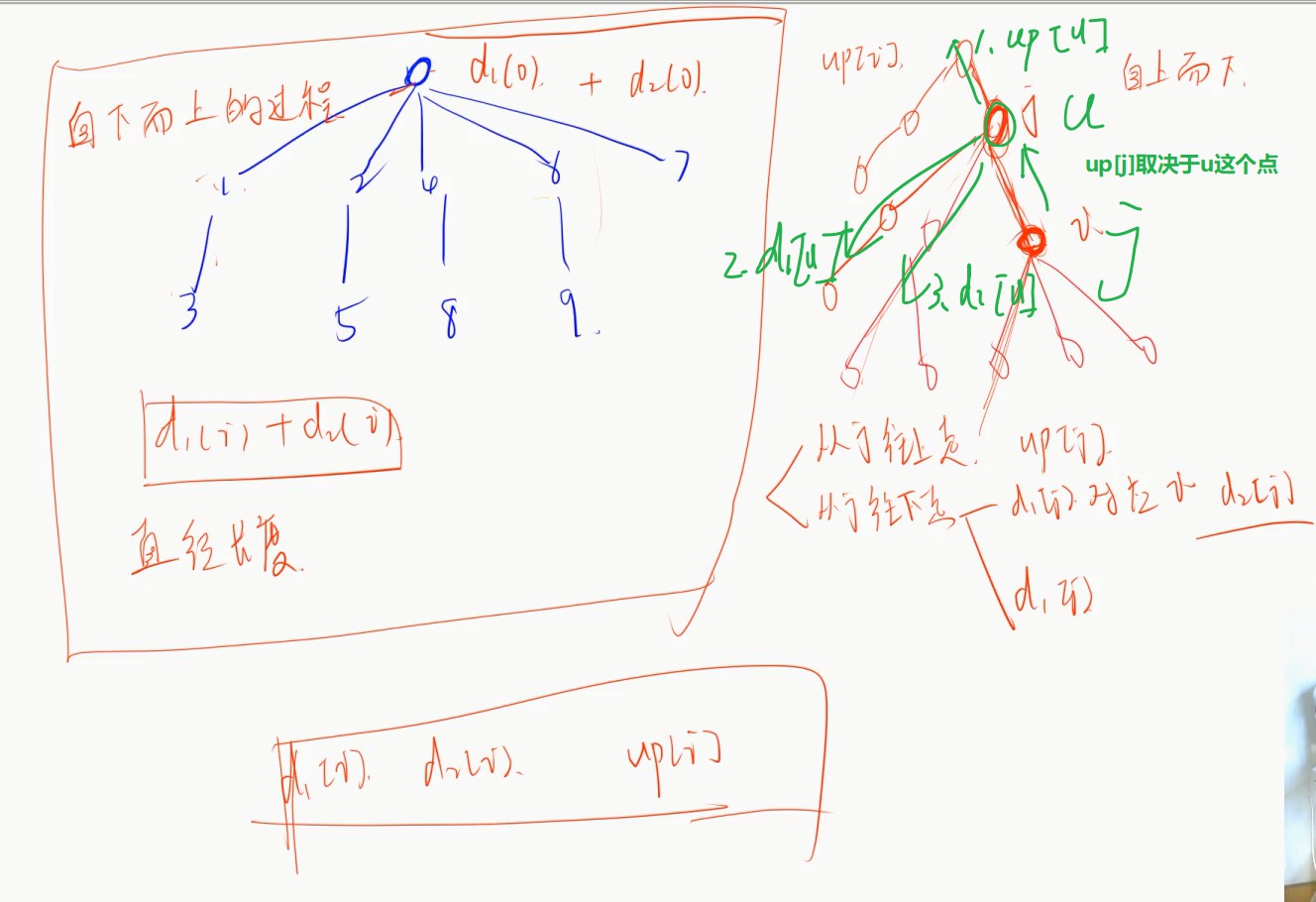
- 往上走怎么求? (取决于
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 200010, M = N * 2;
int n;
int h[N],e[M],ne[M],idx; // 无向图建两条边
int d1[N],d2[N],p1[N],up[N];
int maxd; // 树的直径
void add(int a,int b)
{
e[idx] = b,ne[idx] = h[a],h[a] = idx ++;
}
void dfs_d(int u,int father) // 自底向上更新,先递归
{
for(int i = h[u];~i; i = ne[i])
{
int j = e[i];
if(j != father)
{
dfs_d(j,u);
int d = d1[j] + 1;
if(d > d1[u]){
d2[u] = d1[u], d1[u] = d;
p1[u] = j; // 从u下去得到最大值 下标是j,求up[]有用
}else if(d > d2[u]) d2[u] = d;
}
}
maxd = max(maxd,d1[u] + d2[u]); // 树形DP求树的直径,更新最大值和次大值
}
void dfs_u(int u,int father) // 自顶向下更新,后递归
{
for(int i = h[u];~i;i = ne[i])
{
int j = e[i];
if(j != father)
{
up[j] = up[u] + 1;
if(p1[u] == j) up[j] = max(up[j],d2[u] + 1);
else up[j] = max(up[j],d1[u] + 1);
dfs_u(j,u);
}
}
}
int main()
{
scanf("%d",&n);
memset(h,-1,sizeof h); // 邻接表清空!
for(int i = 0;i < n - 1;i ++ )
{
int a,b;
scanf("%d%d",&a,&b);
add(a,b),add(b,a);
}
dfs_d(0,-1); // 下标从0开始,自底向上更新
dfs_u(0,-1); // 自顶向下更新
for(int i = 0;i < n;i ++ )
{
int d[3] = {d1[i],d2[i],up[i]};
sort(d,d + 3);
if(d[1] + d[2] == maxd) printf("%d\n",i);
}
return 0;
}
判断点是否在直径上,写法,2小呆呆写法
注意:在找次长路径时,还是dfs2(),对于u是次长,但是对于j是最长!
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 200010, M = N * 2;
int n;
int h[N],e[M],ne[M],idx; // 无向图建两条边
int d1[N],d2[N];
int maxd; // 树的直径
bool st[N];
void add(int a,int b)
{
e[idx] = b,ne[idx] = h[a],h[a] = idx ++;
}
void dfs_d(int u,int father) // 自底向上更新,先递归
{
for(int i = h[u];~i; i = ne[i])
{
int j = e[i];
if(j != father)
{
dfs_d(j,u);
int d = d1[j] + 1;
if(d > d1[u]){
d2[u] = d1[u], d1[u] = d;
}else if(d > d2[u]) d2[u] = d;
}
}
maxd = max(maxd,d1[u] + d2[u]); // 树形DP求树的直径,更新最大值和次大值
}
// 从该点往下找最大长度
void dfs2(int u)
{
st[u] = true;
for(int i = h[u]; ~i ;i = ne[i])
{
int j = e[i];
if(d1[u] == d1[j] + 1) dfs2(j);
}
}
// 从该点往下找次大长度
void dfs3(int u)
{
st[u] = true;
for(int i = h[u]; ~i ;i = ne[i])
{
int j = e[i];
if(d2[u] == d1[j] + 1) dfs2(j); // 这里还是dfs2()
}
}
int main()
{
scanf("%d",&n);
memset(h,-1,sizeof h); // 邻接表清空!
for(int i = 0;i < n - 1;i ++ )
{
int a,b;
scanf("%d%d",&a,&b);
add(a,b),add(b,a);
}
dfs_d(0,-1); // 下标从0开始,自底向上更新
for(int i = 0;i < n;i ++ )
{
if(d1[i] + d2[i] == maxd){
dfs2(i);
dfs3(i);
}
}
for(int i = 0;i < n;i ++ )
if(st[i]) printf("%d\n",i);
return 0;
}

