原题链接 https://www.acwing.com/problem/content/124/

题意：

有 $n $个小朋友坐成一圈，每人有 $a[i]$ 个糖果。
每人只能给左右两人传递糖果。
每人每次传递一个糖果代价为$ 1$。
求使所有人获得均等糖果的最小代价。

思路：

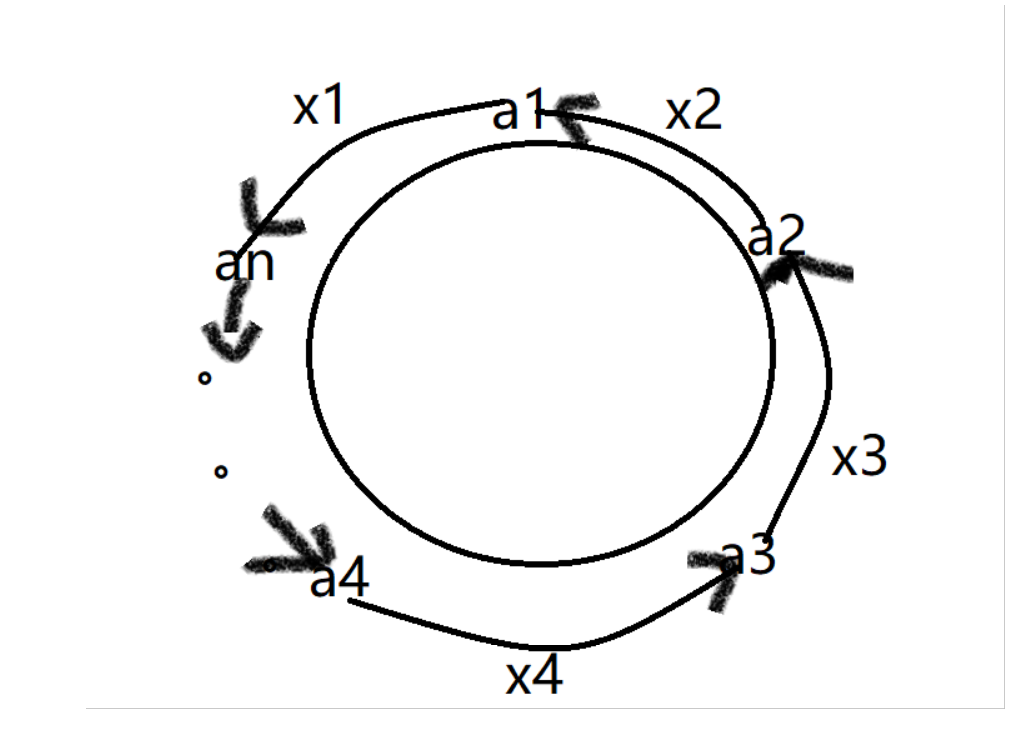
如图：一群小朋友围坐在一起，每个小朋友可以给别人糖果也可以得到别人给的糖果。
假设有一个小朋友a1初始有A1的糖果，他得到了a2的糖果数量计为X2，他自己又给了an小朋友X1数量的糖果。则此时根据题意代价为$X1+X2$。

每个小朋友都会这样（因为$Xn$也可能是0）,因此本题目标便是求$|X1|+|X2|+···+|Xn|$的最小值。

因此可以假设每个小朋友都给别人了，也都接受了。设所有小朋友的糖果平均值是avg。于是便可以依次推出以下三组公式：
(Ai是每个小朋友的初始糖果数量，Xi是给予别人的或者得到别人的)

• I.
  $A1-X1+X2=avg$
  $A2-X2+X3=avg $
  $···$
  $A(n-1)-X(n-1)+Xn=avg$
  $An-Xn+X1=avg$

• II.
  $X1-X2=A1-avg$
  $X2-X3=A2-avg$
  $···$
  $X(n-1)-Xn=A(n-1)-avg$
  $Xn-X1=An-avg$

• III.
  $X1=X1-0$
  $X2=X1-((n-1)avg-A2-A3-···-An)$
  $···$
  $X(n-2)=X1-(3avg-A(n-2)-A(n-1)-An)$
  $X(n-1)=X1-(2avg-A(n-1)-An)$
  $Xn=X1-(avg-An)$
  (从下往上推，依次用X1表示)

再把第三组简化一下就是:
$X1=X1-C1$
$X2=X2-C2$
···
$X(n-1)=X1-C(n-1)$
$Xn=X1-Cn$

因此本题目标$|X1|+|X2|+···+|Xn|$就变成了$|X1-C1|+|X1-C2|+···+|X1-C(n-1)|+|X1-Cn|$
于是根据几何意义本题就成了在C中求一个点X1使得这一点到所有的C的点的距离最小。

根据：
$C1=0$
$C2=((n-1)avg-A2-A3-···-An)$
$···$
$C(n-1)=(2avg-A(n-1)-An)$
$Cn=(avg-An)$
得出C的递推公式为$Ci=C(i-1)-avg+Ai$。

步骤：

综上，本题步骤为：
1.先把每个小朋友的糖果的平均值avg算出来；
2.开辟一个C数组，利用上述求出来的递推公式$Ci=C(i-1)-avg+Ai$算出C数组的值；
3.将计算好的C数组排序；
4.求出中位数C[mid]；
5.循环C数组，计算C数组中的每个数减去该中位数C[mid]的和；
6.输出结果。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>

using namespace std;

typedef long long LL;
const LL N = 1000010;

int n;//表示n个小朋友
LL a[N];//存放每个小朋友的初始的糖果数
LL c[N];
LL res;//表示结果

int main()
{
    //输入数据
    scanf("%d", &n);
    LL sum = 0;
    for (int i = 0; i < n; i ++ )
    {
        scanf("%d", &a[i]);
        sum += a[i];
    }

    //1.先把每个小朋友的糖果的平均值avg算出来    
    LL avg = sum / n;

    //2.利用上述求出来的递推公式Ci=C(i-1)-a+Ai算出C数组的值
    for (int i = 1; i < n; i ++ )
        c[i] = c[i-1] - avg + a[i];

    //3.将计算好的C数组排序   
    sort(c,c + n);

    //4.求出中位数C[mid]
    LL mid = c[n / 2];

    //5.循环C数组，计算C数组中的每个数减去该中位数C[mid]的和
    for (int i = 0; i < n; i ++ )
        res += fabs(c[i] - mid);

    //6.输出结果    
    cout << res << endl;


    return 0;
}