题目描述

给定一位研究者论文被引用次数的数组（被引用次数是非负整数），数组已经按照 升序排列 。编写一个方法，计算出研究者的 h 指数。

h 指数的定义: “h 代表“高引用次数”（high citations），一名科研人员的 h 指数是指他（她）的 （N 篇论文中）总共有 h 篇论文分别被引用了至少 h 次。（其余的 N - h 篇论文每篇被引用次数不多于 h 次。）”

样例

输入: citations = [0,1,3,5,6]
输出: 3 
解释: 给定数组表示研究者总共有 5 篇论文，每篇论文相应的被引用了 0, 1, 3, 5, 6 次。
     由于研究者有 3 篇论文每篇至少被引用了 3 次，其余两篇论文每篇被引用不多于 3 次，所以她的 h 指数是 3。

题目要求至少h个数大于等于h
两种模板均可，但是在不同的模板选取的l和r含义不同，解决思路不一样。

算法1

[二分版本Ⅰ](https://www.acwing.com/blog/content/31/

按照模板首先确定l = 0， r = n-1; 这样选择范围是在整个数组下标区间内二分来找目标值， 最终返回篇数为 citation.length - mid;

选择的性质是满足 条件：引用数大于等于论文数 中最小的下标i; 相当于找绿色区域最左端作为目标值所以是版本Ⅰ
check(): citation[mid] >= citation.length - mid

因为这种情况没有直接去搜索最优解，而是找到下标通过运算得到结果，因为需要考虑当数组不存在的时候或者数组内的值均为0的情况
考虑样例[0] [0, 0],这两种情况搜索到下标均为0，但是返回结果为1， []这种情况会直接返回 -1，因此需要特判。

java代码

public int hIndex(int[] citations) {
        if(citations.length == 0 || citations[citations.length - 1] == 0) return 0;
        int l = 0, r = citations.length - 1;
        while(l < r){
            int mid = l + r >> 1;
            if(citations[mid] >= citations.length - mid ) r = mid;
            else l = mid + 1;
        }
        return citations.length - l;
    }

算法2

(二分版本Ⅱ)

如果确定l = 0, r = n 这种确定范围的方式就是直接去寻找答案，结束二分的值就是要求的h
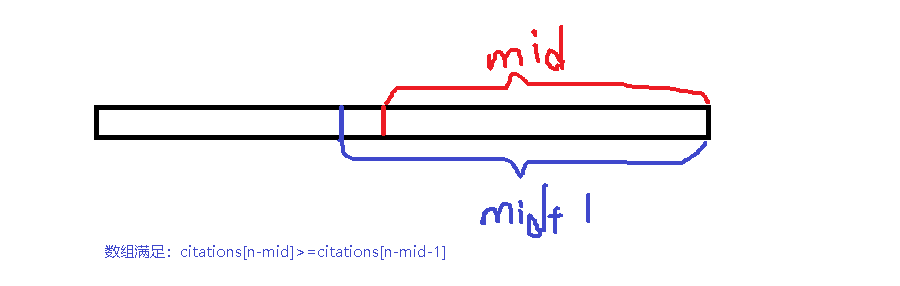
这种方式的依据是：如果mid满足 有mid个数大于等于mid，那么一定有mid+1个数大于等于k(k <= mid)
但是我们要选择mid尽可能大，所以相当于找红色区域的最右端所以是版本Ⅱ

Java 代码

public int hIndex(int[] citations) {
        int l = 0, n = citations.length, r = n;
        while(l < r){
            int mid = l + r + 1>> 1;
            if(citations[n - mid] >= mid) l = mid;
            else r = mid - 1;
        }
        return r;
    }