题目描述

给定一个整数 n，将数字 1∼n 排成一排，将会有很多种排列方法。

现在，请你按照字典序将所有的排列方法输出。

输入格式
共一行，包含一个整数 n。

输出格式
按字典序输出所有排列方案，每个方案占一行。

数据范围
1≤n≤7
输入样例：
3
输出样例：
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

算法:dfs

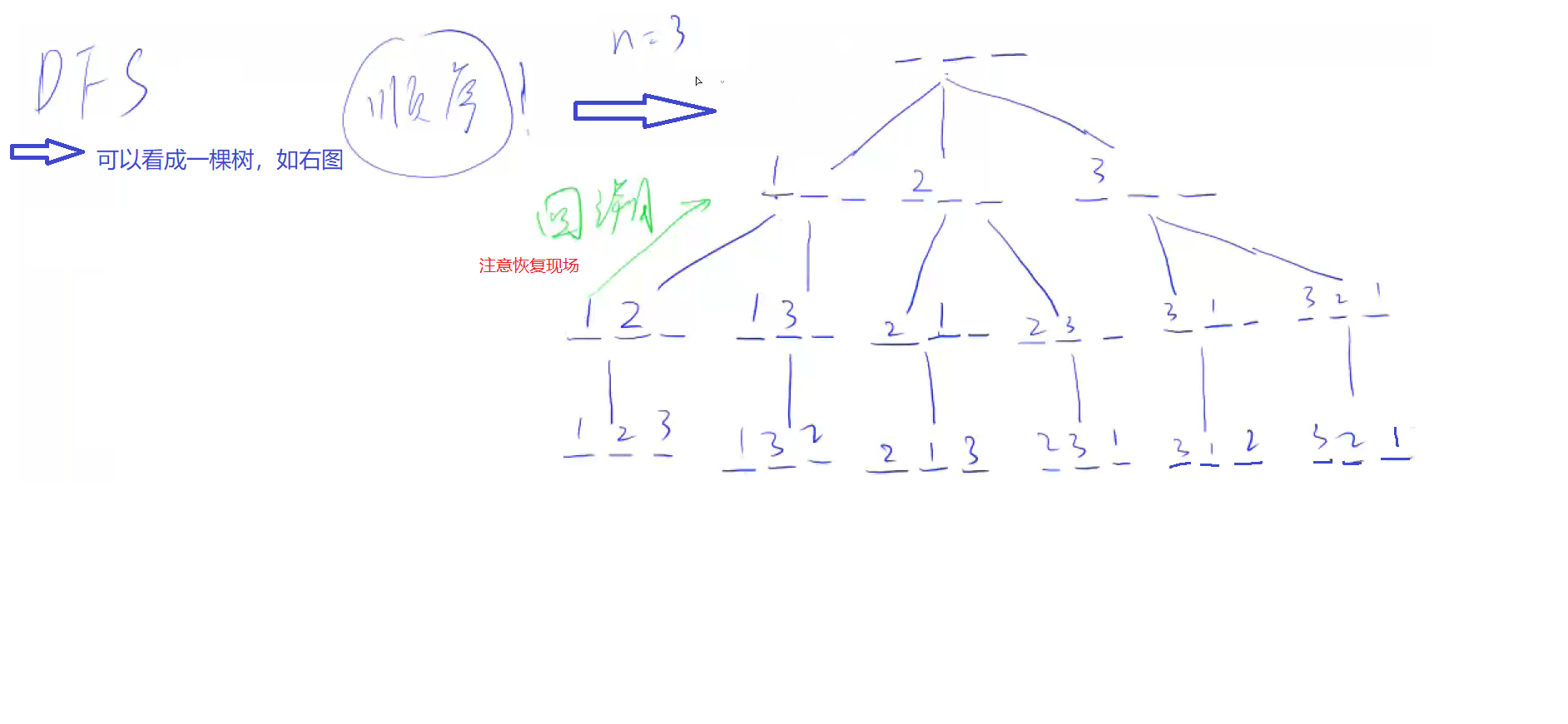
参考文献

y总

C++ 代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 10;
//整数n
int n;
//path数组记录一种方案
int path[N];
//bool标记该位置的点是否被用过（true为用过）
bool st[N];

void dfs(int u){
    //当u=n的时候，说明已经搜索到最后一层了，这时候只要输出path数组里面的记录的路径即可
    if(u == n){
        for(int i = 0 ; i < n ; i++) printf("%d " , path[i] );
         puts("");
        return;
    }

    //当u小于n的时候，说明还没有搜索完，所以要枚举一下当前位置可以填哪些数
    for(int i  = 1 ; i <= n ; i++){
        //如果当前位置为false，说明这个位置可以填入数字。false取反之后为true，符合条件
        if(!st[i]){
            //把i放入到当前这个位置上去
            path[u] = i;
            //同时记录这个位置已经被用过了
            st[i] = true;
            //处理完当前这一层之后，开始搜索下一层
            dfs(u + 1);
            //当dfs函数搜索完下面所有的层数之后，回到当前层，要恢复成原来的状态，方便
            //下一次的搜索
            /*path[u] = 0;思考一下可以看出，path数组这个不需要恢复，因为每一次搜索的时候
            这个位置上的数都会被覆盖掉，不影响结果。
            但是st标记数组需要恢复，因为每一次都需要他来进行判断当前这个位置可不可以进行
            填值
            */
            st[i] = false;
        }
    }
}

int main(){
    cin >> n;
    //从第0个位置开始搜索
    dfs(0);

    return 0;
}