分析

• 本题需要用到扫描线技巧。我们可以统计出所有矩形对应四个顶点的横坐标，过这些横坐标做x的垂线（即扫描线），如下图：

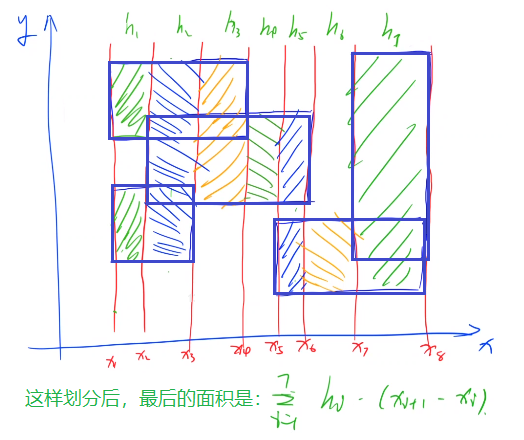
• 在沿着扫描线从左向右扫描的过程中，我们可以求解每个h的大小，我们可以这样操作：对于每个矩形与y轴平行的两个边，左边的权值记为+1，右边的权值记为-1（如下图）：

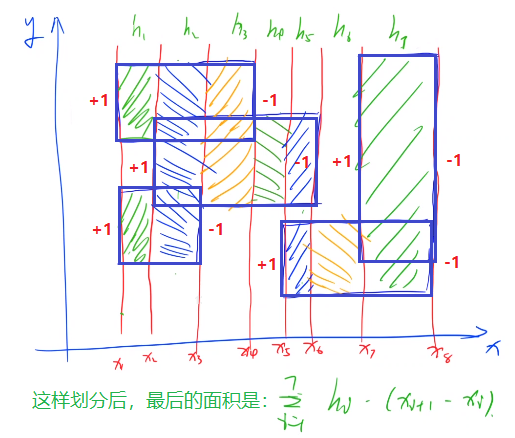
• 如果当前扫描线上是+1的话，将沿y轴方向的对应区间全部加上1，如果是-1的话，全部加上-1（区间上对应的数表示当前区间被多少个矩形覆盖）；为了求出对应的h，我们需要统计出沿y轴的整个区间内大于0的区间长度总和；因此，总结一下，我们存在两个操作：

（1）对于某个区间加上一个数；

（2）统计出整个区间中大于0的区间的长度和；

• 上面的操作对应区间修改、区间查询，因此可以使用线段树来求解，线段树中每个节点存储的信息如下：

struct Node {
    int l, r;  // 区间左右端点，这里是纵坐标离散化后对应的值，是整数
    int cnt;  // 当前区间[l, r]全部都被覆盖的次数
    // 不考虑祖先节点cnt的前提下，只考虑当前节点及子节点，cnt>0的区间总长度，类似于刚才(aAcwing 243)的sum
    double len;
}

• 此时，本题的基本做法已经讲解完毕，但是我们维护cnt和len比较麻烦，所以我们考虑是否能根据此问题的性质进行优化，最终优化的结果是我们不需要进行pushdown操作，分析如下：

• 我们注意到本题中的线段树具有如下性质：

（1）因为我们求扫描线上总高度h，所以我们在查询的时候只会使用到根节点的信息；可以看到query的基本结构如下：

int query(int u, int l, int r) {
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum;  // 对于本题，这句话一定会被执行，因此pushdwon执行不到

    pushdown(u);
    // ......
}

从上面的代码中我们发现，query中的pushdown永远不会被执行到。

（2）因为矩形存在两条边和y轴平行，因此线段树中所有的操作一定都是成对出现的（所谓成对出现，指的是我们对于某个区间加上一个1，则一定会在之后的操作中再将同样的一个区间减去一个1），且先加后减。可以看到modify的基本结构如下：

void modify(int u, int l, int r, LL d) {
    if (tr[u].l >= l && tr[u].r <= r) {
        tr[u].sum += (LL)(tr[u].r - tr[u].l + 1) * d;
        tr[u].add += d;
    } else {
        pushdown(u);  // 这句话是多余的
        // ......
        pushup(u);
    }
}

核心：操作的区间是相同的，且先加1后减1。假设modify是给某个区间减1，则这之前这个区间一定都被加过1，对应线段树中的节点（是个集合，记为A）一定有该懒标记，减1的时候一定再会将A中所有的懒标记恢复到加1前的状态，因此，没必要把当前父节点的修改信息下传到子节点，也就是没必要使用pushdown操作。

• 这一题不用pushdown是因为这个题目十分特殊，可以说这种做法就是针对这个题目的，因此可以单独记下来。

• 另外这一题中坐标都是小数，我们存储纵坐标的时候需要进行离散化，这里使用vector对纵坐标进行离散化。因为图中有n个矩形，所以平行于y轴的边有$2n$条，因此我们需要存储$2n$个区间，每个区间（平行于y轴的线段）存储一个横坐标，两个纵坐标，并且需要按照横坐标从小到大的顺序排序，存储线段可以使用结构体，如下：

struct Segment
{
    double x, y1, y2;  // 区间的两个端点为(x, y1), (x, y2)
    int k;  // k只能取+1或者-1，表示当前区间的操作是+1还是-1
    bool operator< (const Segment &t) const {  // 让结构体可以从小到大排序
        return x < t.x;
    }
}

• 我们线段树中维护的内容是一个个的区间，一共$2n$个，因此线段树大小要开到$8n$的大小。

• 这些区间的纵坐标需要放到ys（是一个vector）中，进行离散化（保序离散化，因为我们要判断区间的包含关系），离散化过程：排序，去重；然后通过lower_bound可以找到每个y在vector中的下标；ys[0]表示最小的一个纵坐标值。

• 线段树中需要维护$2n$个区间，因此线段树中的每个节点代表一个区间，假设某个区间是是$(y_i, y_{i+1})$，且$y_i$和$y_{i+1}$之间没有其他的y了，则该区间对应于线段树中的叶节点，则如果$ys[l1]=y_i, ys[r1]=y_{i+1}$，对应的线段树的区间是$[l1, r1]$，另外注意这里的$(y_i, y_{i+1})$可能不是矩形的某条边，如上图中扫描线$x_8$对应的情况。这里的$x_8$对应线段树中的三个区间（只单纯的考虑后面两个矩形的情况下是3个，否则不是）

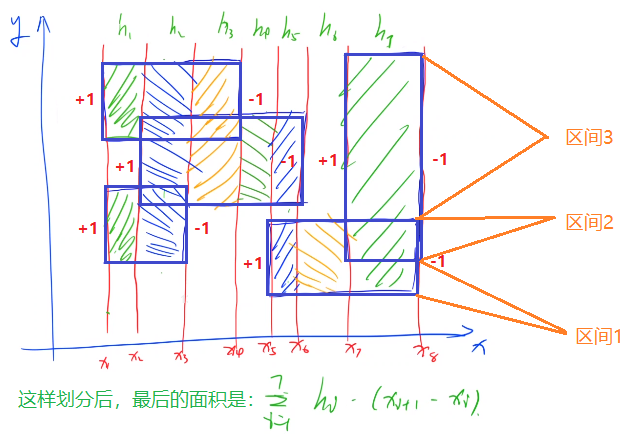
• 具体来说，上图中存在的最小区间个数为8个，因此线段树中的叶节点也是8个：

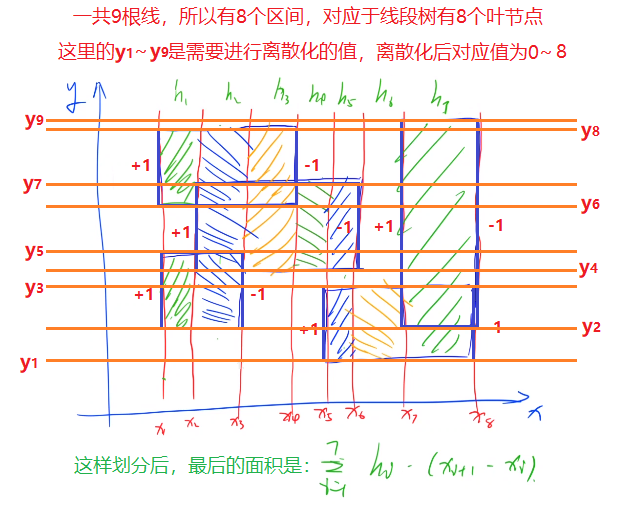
• 因此线段树中的某个”点”对应于图中是某段区间，比如根节点对应于上图中的区间$[y_1, y_8]$。

• 线段树中u这个节点表示的是$[tr[u].l, tr[u].l + 1]$，$tr[u].l + 1, tr[u].l + 2]$， ......， $[tr[u].r, tr[u].r + 1]$这些小区间，这里的$tr[u].l,tr[u].r$都是对应y离散化后的值。

• 如上图，这些小区间分别是$[y_1, y_2]、[y_2, y_3]、…、[y_8, y_9]$，他们的长度组成一个数组a，其中a[0]表示第一个区间的长度，对应离散化区间为[0,1]，原区间为[ys[0], ys[0+1]]=$[y_1, y_2]$。

• a[0~2]表示第一个区间的长度，对应离散化区间为[0,1]、[1, 2]、[2, 3]，原区间为[ys[0], ys[2+1]]=$[y_1, y_4]$。

• 那么我们的线段树相当于对数组a进行区间修改、区间查询，例如：

• 当我们要更新$[y_4, y_7]$这一段区间，相当于更新a[3~5]，对应于$a[find(y_4) - (find(y_7)) - 1]$（find函数返回离散化后的值）。

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

const int N = 100010;

int n;  // 矩形个数
struct Segment {
    double x, y1, y2;  // 区间的两个端点为(x, y1), (x, y2)
    int k;  // k只能取+1或者-1，表示当前区间的操作是+1还是-1
    bool operator< (const Segment &t) const {
        return x < t.x;
    }
} seg[N * 2];  // 存储区间

struct Node {
    int l, r;  // 纵坐标对应的离散化的值
    int cnt;  // 当前区间[l, r]全部都被覆盖的次数
    // 不考虑祖先节点cnt的前提下，只考虑当前节点及子节点，cnt>0的区间总长度
    // 类似于刚才(aAcwing 243)的sum
    double len;
} tr[N * 8];

vector<double> ys;  // 用于离散化纵坐标

int find(double y) {
    return lower_bound(ys.begin(), ys.end(), y) - ys.begin();
}

void pushup(int u) {

    if (tr[u].cnt) {  // 说明节点u对应的区间完全被覆盖
        // 例如tr[u].l = 3, tr[u].r = 5, 对应上面分析的于a[3],a[4],a[5]三个区间
        // 对应离散化区间为[3, 4], [4, 5], [5, 6]
        // 对应上面的[ys[3], ys[4]], [ys[4], ys[5]], [ys[5], ys[6]]
        // 即[y4, y5], [y5, y6], [y6, y7]
        tr[u].len = ys[tr[u].r + 1] - ys[tr[u].l];
    } else if (tr[u].l != tr[u].r) {  // 没有完全被覆盖，且有子区间
        tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
    } else {  // 没有完全覆盖，且是叶节点
        tr[u].len = 0;
    }
}

void build(int u, int l, int r) {

    tr[u] = {l, r, 0, 0};
    if (l != r) {
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
    }
}

// 从节点u开始将区间[l, r]加上k
void modify(int u, int l, int r, int k) {

    if (tr[u].l >= l && tr[u].r <= r) {
        tr[u].cnt += k;
        pushup(u);
    } else {
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) modify(u << 1, l, r , k);
        if (r > mid) modify(u << 1 | 1, l, r, k);
        pushup(u);
    }
}

int main() {

    int T = 1;
    while (scanf("%d", &n), n) {

        ys.clear();
        for (int i = 0, j = 0; i < n; i++) {
            double x1, y1, x2, y2;
            scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
            seg[j++] = {x1, y1, y2, 1};
            seg[j++] = {x2, y1, y2, -1};
            ys.push_back(y1), ys.push_back(y2);
        }

        // 对纵坐标进行离散化
        sort(ys.begin(), ys.end());
        ys.erase(unique(ys.begin(), ys.end()), ys.end());

        // ys.size()个纵坐标，ys.size()-1个区间，下标是0~ys.size() - 2
        build(1, 0, ys.size() - 2);
        // 按照横坐标排序(横坐标当成扫描线)
        sort(seg, seg + n * 2);

        double res = 0;
        for (int i = 0; i < 2 * n; i++) {
            if (i > 0) res += tr[1].len * (seg[i].x - seg[i - 1].x);
            modify(1, find(seg[i].y1), find(seg[i].y2) - 1, seg[i].k);
        }

        printf("Test case #%d\n", T ++ );
        printf("Total explored area: %.2lf\n\n", res);
    }

    return 0;
}