Blog
题目
思路 1

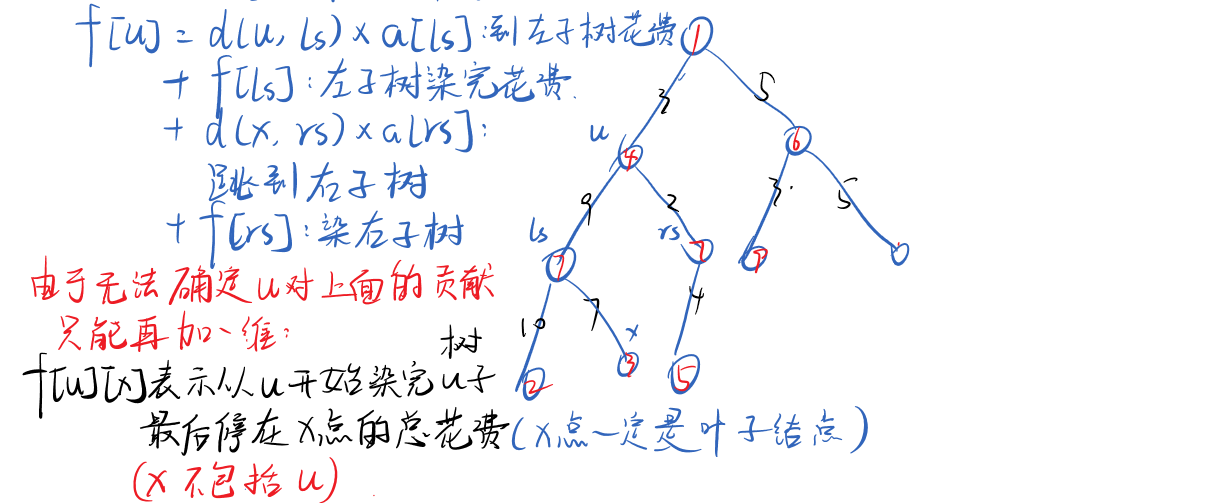




代码 1
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#define int long long
using namespace std;
const int N = 200010, INF = 2e18;
// 定义 A 为点权, B[i] 为 i 连向父亲的点权
int n, A[N], B[N], dep[N];
// 由于开数组需要 n * n 的空间, 但是实际上不需要那么多, 所以动态加状态
vector<int> f[N], g[N], dis[N];
inline void update(int u) {
// 枚举所有祖先
for (int i = u; i >= 1; i >>= 1)
f[i].push_back(0), g[i].push_back(0),
dis[i].push_back(dep[u] - dep[i]);
}
#define ls (u << 1)
#define rs (u << 1 | 1)
void DFS(int u) {
// 没有左儿子, 说明 u 是叶子节点
if (ls > n) { update(u); return; }
dep[ls] = dep[u] + B[ls], DFS(ls);
// 此时只有一个左儿子, 没有右儿子
if (rs > n) {
update(u);
f[u][0] = A[ls] * B[ls], f[u][1] = INF;
g[u][0] = f[u][0], g[u][1] = A[u] * B[ls];
return;
}
dep[rs] = dep[u] + B[rs], DFS(rs);
int sz = f[ls].size(); // 左儿子的叶子节点个数, 后面有用
int fls = INF, frs = INF, gls = INF, grs = INF;
// d[u][rs] = B[rs], d[u][ls] = B[ls];
// 其中 d[ls][y] 由于 ls存的是子树, 没存 y, 所以变型等于 dis[u][y] + B[ls]
// d[rs][y] 同理
// 这里把状态转移方程重写一遍, 避免读者上下翻看
// f[u][x] = f[ls][x] + min { B[rs] * A[rs] + (dis[u][y] + B[ls]) * A[ls] + f[rs][y] }
// frs = min { B[rs] * A[rs] + (dis[u][y] + B[ls]) * A[ls] + f[rs][y] };
// f[u][x] = f[rs][x] + min { B[ls] * A[ls] + (dis[u][y] + B[rs]) * A[rs] + f[ls][y] }
// fls = min { B[ls] * A[ls] + (dis[u][y] + B[rs]) * A[rs] + f[ls][y] }
for (int y = 0; y < f[u].size(); y++)
if (y < sz) fls = min(fls, B[ls] * A[ls] + (dis[u][y] + B[rs]) * A[rs] + f[ls][y]);
else frs = min(frs, B[rs] * A[rs] + (dis[u][y] + B[ls]) * A[ls] + f[rs][y - sz]);
// y 在右子树 因为右子树大小限制, y 都要减去 sz
for (int x = 0; x < f[u].size(); x++)
if (x < sz) f[u][x] = f[ls][x] + frs;
else f[u][x] = f[rs][x - sz] + fls;
// g[u][x] = f[ls][x] + min { g[rs][y] + dis[u][y] * A[u] + B[ls] * A[ls] }
// grs = min { g[rs][y] + dis[u][y] * A[u] + B[ls] * A[ls] }
// g[u][x] = f[rs][x] + min { g[ls][y] + dis[u][y] * A[u] + B[rs] * A[rs] }
// gls = min { g[ls][y] + dis[u][y] * A[u] + B[rs] * A[rs] }
for (int y = 0; y < f[u].size(); y++)
if (y < sz) gls = min(gls, g[ls][y] + dis[u][y] * A[u] + B[rs] * A[rs]);
else grs = min(grs, g[rs][y - sz] + dis[u][y] * A[u] + B[ls] * A[ls]);
for (int x = 0; x < f[u].size(); x++)
// f[u][x] 即为漏的那种情况
if (x < sz) g[u][x] = min(f[u][x], f[ls][x] + grs);
else g[u][x] = min(f[u][x], f[rs][x - sz] + gls);
}
signed main() {
cin >> n;
for (int i = 1; i <= n; i++) cin >> A[i];
for (int i = 2; i <= n; i++) cin >> B[i];
DFS(1);
long long res = 2e18;
for (int x = 0; x < g[1].size(); x++) res = min(g[1][x], res);
cout << res << endl;
return 0;
}
思路 2




代码 2
#include <iostream>
#include <cstring>
#include <algorithm>
#define int long long
using namespace std;
const int N = 200010, INF = 2e18;
int n, m, layer[N], A[N], B[N], d[N][20];
int f[N][20], g[N][20];
#define ls (i << 1)
#define rs (i << 1 | 1)
int DP() {
for (int i = n; i >= 1; i--) {
for (int j = 1; j <= layer[i]; j++) {
int brother = (i >> j - 1) ^ 1;
if (ls > n) f[i][j] = d[i][j] * A[i >> j],
g[i][j] = (d[i][j] + d[brother][1]) * A[brother];
else if (rs > n) f[i][j] = d[ls][1] * A[ls] + f[ls][j + 1],
g[i][j] = d[ls][1] * A[ls] + g[ls][j + 1];
else f[i][j] = min(d[ls][1] * A[ls] + g[ls][1] + f[rs][j + 1],
d[rs][1] * A[rs] + g[rs][1] + f[ls][j + 1]),
g[i][j] = min(d[ls][1] * A[ls] + g[ls][1] + g[rs][j + 1],
d[rs][1] * A[rs] + g[rs][1] + g[ls][j + 1]);
}
}
int res = INF;
for (int i = 1; i <= n; i++) {
int temp = f[i][1];
int x = i, y = i ^ 1, fa = x >> 1;
for (int j = 1; j <= layer[i]; j++) {
if (y <= n) temp += d[y][1] * A[y] + f[y][2];
else temp += d[fa][1] * A[fa >> 1];
x = fa, y = x ^ 1, fa = x >> 1;
}
res = min(res, temp);
}
return res;
}
signed main() {
cin >> n;
for (int i = 1; i <= n; i++) cin >> A[i];
for (int i = 2; i <= n; i++) cin >> B[i];
// 找层
for (int i = 1; i <= n; i++) layer[i] = layer[i >> 1] + 1;
// 算距离
for (int i = 2; i <= n; i++)
for (int j = 1; j <= layer[i]; j++)
d[i][j] = d[i >> 1][j - 1] + B[i];
cout << DP() << endl;
return 0;
}

