双向bfs广搜解法（思路分析超详细+视频讲解）

由于本蒟蒻看到大家都用的 A* 解法，所以想试试双向bfs能不能做，理论上是可以的，不过确实也是可行的，所以想和大家分享一下一个新的解法，不过该解法代码可能比较复杂，但是思路比较清晰易懂

文章最后有视频讲解链接！！

算法思路：

1、与传统的双向bfs广搜的算法思路是一致的，由于我们是从某一个状态变化到另外一个状态，如果单向bfs的话状态可能会很多很多，所以我们采用双向搜索，可以很大程度上的减少我们的计算量

2、那这个时候可能会有同学问了，比如有这么一个现实的问题，小明家距离学校1000m，无论小明怎么走，他走的总路程不应该都是1000m吗，所以由此是不是可以推出双向和单向所走过的路程是一样的呢？

3、答案是否定的。这种问题显然不是简单的生活实际问题，在生活实际中，我们如果距离学校直线距离为1000m，那么确实没有办法优化了，但是我们的算法题里面却并非如此。

4、何出此言？显然 没有显然，我们要杜绝“显然”这个词（和y总学的hh）。我们这道题，是通过一个搜索的方式去做的，何为搜索？就是我们会寻找每一条有可能到达终点的路径，那么这种路径就太多了，而且每种路径也只是可能到而已，并不是说每条路径都能到的。

5、那么路径到底有多少呢？我们可以大概算一下，就拿本题而言，我们有4个移动操作，假设我们从起点转移到终点至少需要 n 步，那么最起码我们要搜索 $4^n$ 条路径，而且这已经是很理想的状况了，我们在搜索的时候难免会“走几条弯路”（也就是搜那些不可能到的路径，而且搜了很长一段距离停不下来），那么时间复杂度就会达到一个指数级别的增长，我大概估计了一下最起码有几百亿甚至更多条路径。

6、而我们知道C++一秒大概是跑一亿次左右，那么对于本题而言如此巨大的搜索量是完全行不通的。

7、那么这个时候我们引入双向搜索，就可以达到完美的优化。不过说了这么多好像没有解释为什么能优化？那么请看下面这张图：

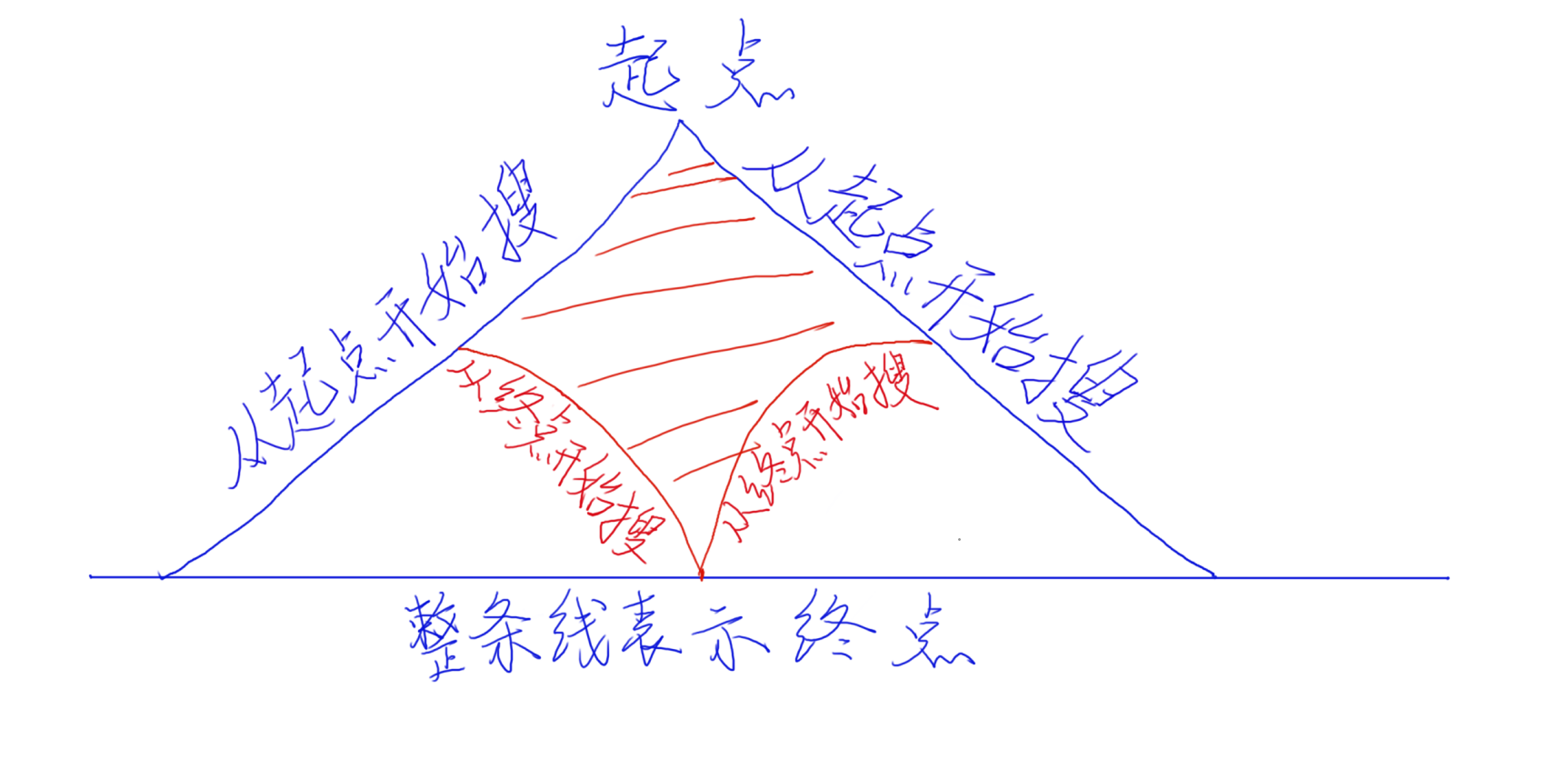
8、上图描述了两种情况，只从起点开始搜和起点和终点同时开始搜，可以明显看出，如果只从起点开始搜的话，我们需要搜索的面积将会是蓝色线包围起来的像一座小山一样的面积。但是如果我们从终点和起点同时开始搜的话，那么我们搜索的面积只有图中红色的范围（画的不够形象，其实差别应该是很大的，意思意思hh）

9、所以这就是我们双向搜索能够优化的原因。

10、再具体一些呢？双向搜索能让我们少走很多不不要走的弯路，也就是一些永远也到不了的分支我们不需要去搜了，这就省了很多不必要的计算。

11、那好了，那么具体的，双向搜索是如何实现的呢？

12、大致过程是这样的，我们分别从起点和终点开始搜索状态，当我们发现两边搜到了相同的状态（记为中间状态）的时候，那就意味着我们搜到了一条路，能够使得我们能从起始状态走到状态，再从中间状态走到终点。而且此时我们是第一次搜到，所以这一定是最优解，那么我们就可以直接返回，然后输出了。

大致的思路我们现在已经有了，我们现在来把我们的思路落实到我们的具体的代码上

1、我们先来看一下我们题目中需要注意的几个问题。第一个，如何表示状态？第二个，如何对状态进行操作？第三个，如何记录我们的路径（也就是我们每次执行操作的情况）？第四个，如何实现双向搜索？第五个，如何判断我们当前已经找到中间状态了呢？

2、那么我们现在来一一解决这些问题。

3、如何表示状态？我们现在的状态是一个二位数组的形式，如果一直用二维的数组来存储的话，未免过于麻烦，我们不妨就利用题中已经给出的信息，来设计我们的状态。比如下图所示的一些情况：

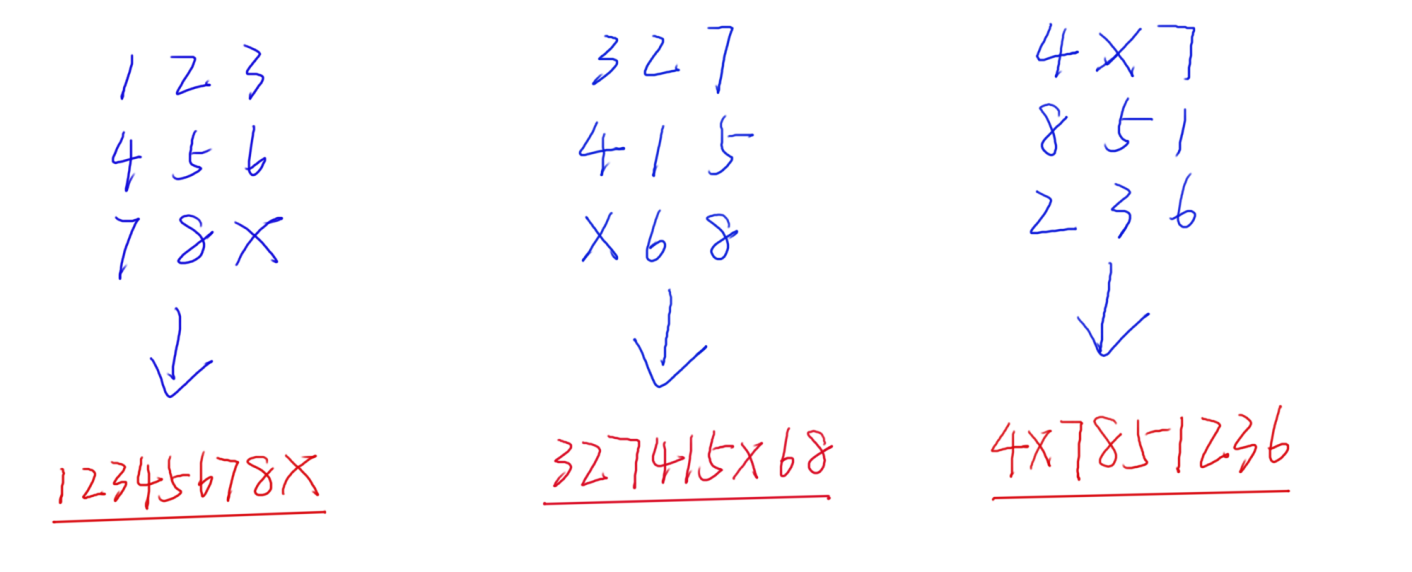
4、如上图所示，我们按照顺序，从第一行到第三行，依次将每个字符连接，得到一个字符串，那么我们就以该字符串表示我们当前的状态。

5、那么我们如何对于状态执行我们的操作呢？这个的话就稍微麻烦一点吧，我们需要在每次执行操作的时候，将我们的状态，也就是一个字符串，转化为原来的字符数组，然后进行操作，最后在把字符数组转回我们的字符串。（不过这里也只是代码上面略显繁琐，时间复杂度还是很低的）

6、那么如何记录我们的路径呢？记录路径的时候，我们需要这么操作：

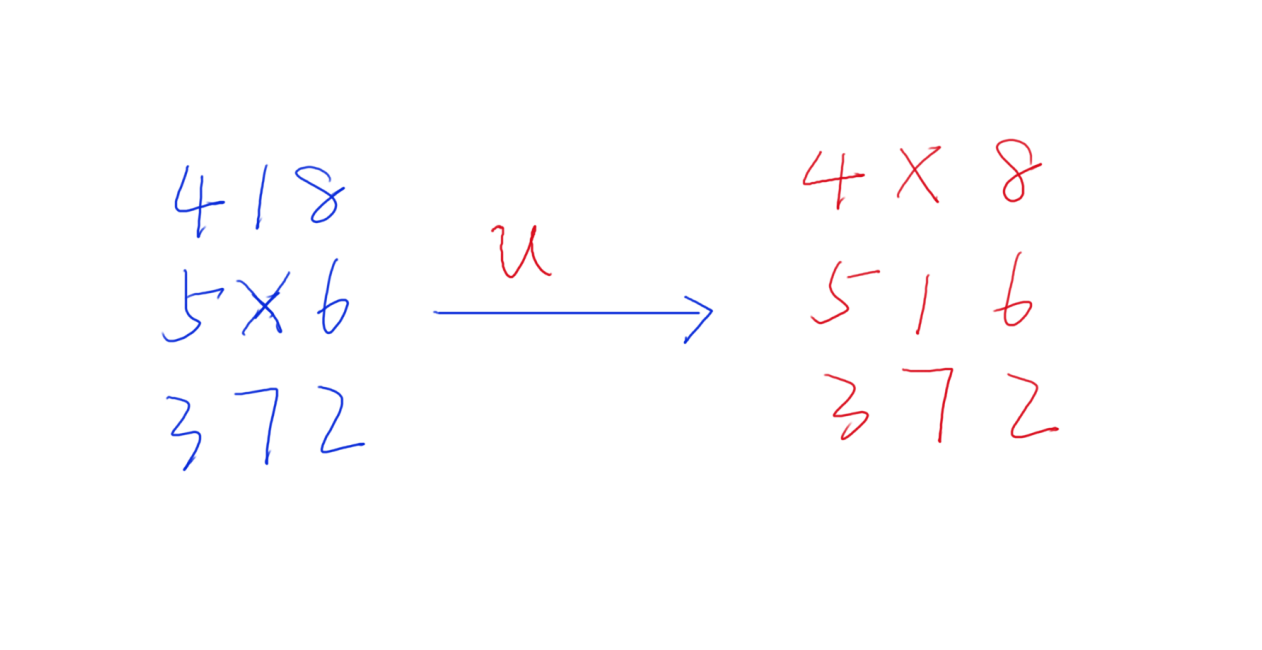
7、如上图所示，我们进行了 ‘u’ 操作，也就是让 x 与其上面的元素交换，得到了一个新的状态。那么我们此时记录一下我们当前状态是由哪个状态转移过来的，以及转移的时候记录了什么操作，就可以了，到最后我们再按照这样的逻辑就可以得到整条路径。这里其实是比较难理解的，因为比较抽象，我还是举个例子给大家看一下，具体一点会好一些。

8、上图的例子是，我们当前有 A,B,C,D,E,F,G 这么一些状态，我们的目标是从 A 到 G，然后实际的路线如上图所示，那么我们根据我们之前说的存储方式，就有如下存储对应关系：

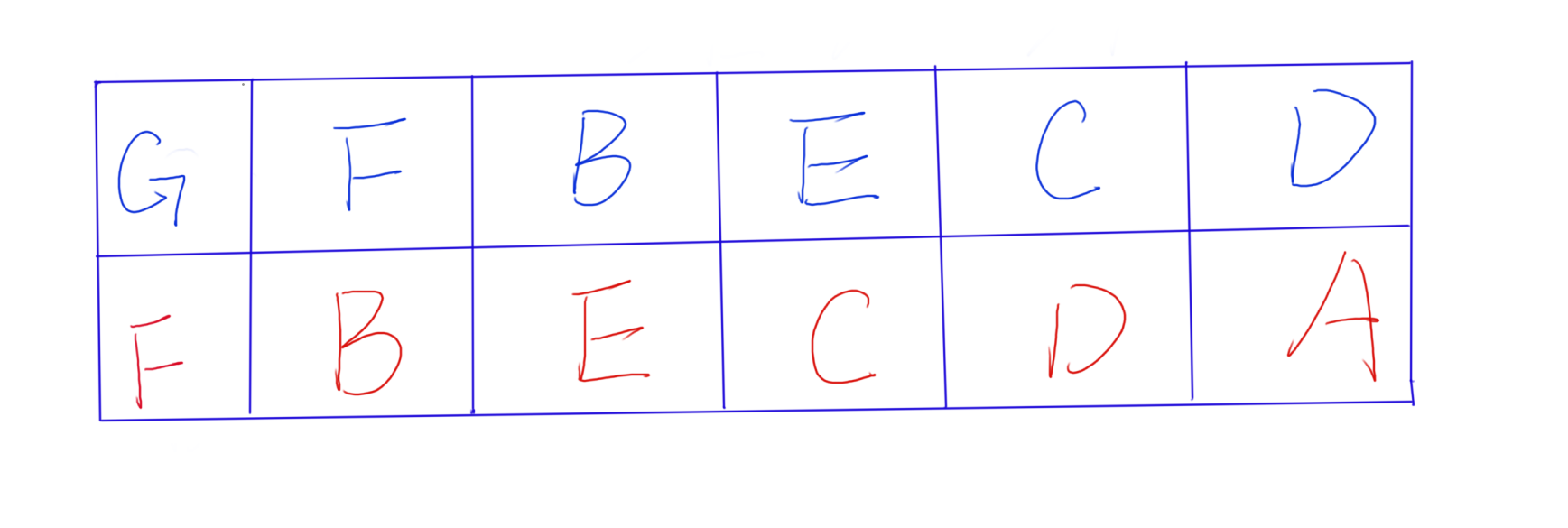
9、G 是从 F 过来的，所以它存的是 F ，F 是从 B 过来的所以它存的是 B ，以此类推。那么我们如何取出这条路径呢？那就是每次都交换迭代一下，让我们当前的状态变成我们当前存储的状态，那么一直迭代下去就可以到达我们的初始状态。

10、下一个问题，如何实现双向搜索呢？那么其实这一步仔细想一下应该不难，双向搜索和单向搜索其实差别不大，只是多了一个队列，然后多扩展一个队列就好了。不过这个地方有一个小小的优化，那就是我们每次都扩展队列中元素较少的的那一个队列，这样就可以让我们两个队列的元素维持在一个平衡状态，进而能减少那些不必要的搜索（因为如果偏向一边搜索的话，会搜到很多不必要的路径，平衡一点才能更快找到中间状态）

11、对了，还有一个细节补充一下，我们搜索的条件是我们当前两个队列中都含有元素，如果其中一个队列中不包含元素了，同时我们当前还是没有找到中间状态了，那么就说明我们此时没有中间状态，也就是无解。如果大家觉得比较抽象那么可以看一下下面这张图示：

12、图中表示从终点出发的搜索已经全部搜完了，但是我们还是没有找到中间状态，那么我们从终点出发的路径就会形成类似一个闭环，不会与起点出发的搜索有公共路径了。

13、最后一个问题，如何判断我们当前已经找到中间状态了呢？我们在搜索的时候，可以记录一下我们当前状态到我们各个搜索状态起点（也就是起点和终点）的距离，如果某个状态到搜索状态起点的距离不为0（除起点状态外），那么就说明我们已经搜到过这个状态了，那么我们对应的看一下对方搜索路径中有没有搜到这个状态（也就是该状态到另外一个搜索起点的距离是否为0），如果该状态到两个起点的距离都不为0，也就是说它被二者都搜到过了，那么它就是我们需要的中间状态。

14、那么以上的基本问题到这里我们都已经解决了，那么本题目还有一些比较特殊的问题。

15、第一个，由于本题的搜索量是在太大太大，以至于双向搜索的优化可能都无法彻底解决（比如一些无解的情况，搜索量趋近于无穷，不可能通过简单的搜索实现）。所以这里就要利用一些定理以及性质，来对于无解的情况进行一些特判，以达到过题的效果。比如在后续的代码中我们可以发现，我们在搜索过程中加入了一个特判：当我们搜索的元素过多的时候，其实也就意味着我们当前的情况是无解的，那就直接退出。

16、在我们最后的取出路径的时候，需要注意一个很重要的问题。（在我们最后一步取出路径的时候）由于我们有一条路线是从终点状态搜到中间状态的，那么我们需要得到从中间状态得到终点状态的时候，并不是简单的倒回来操作就可以的。比如下面这个例子：

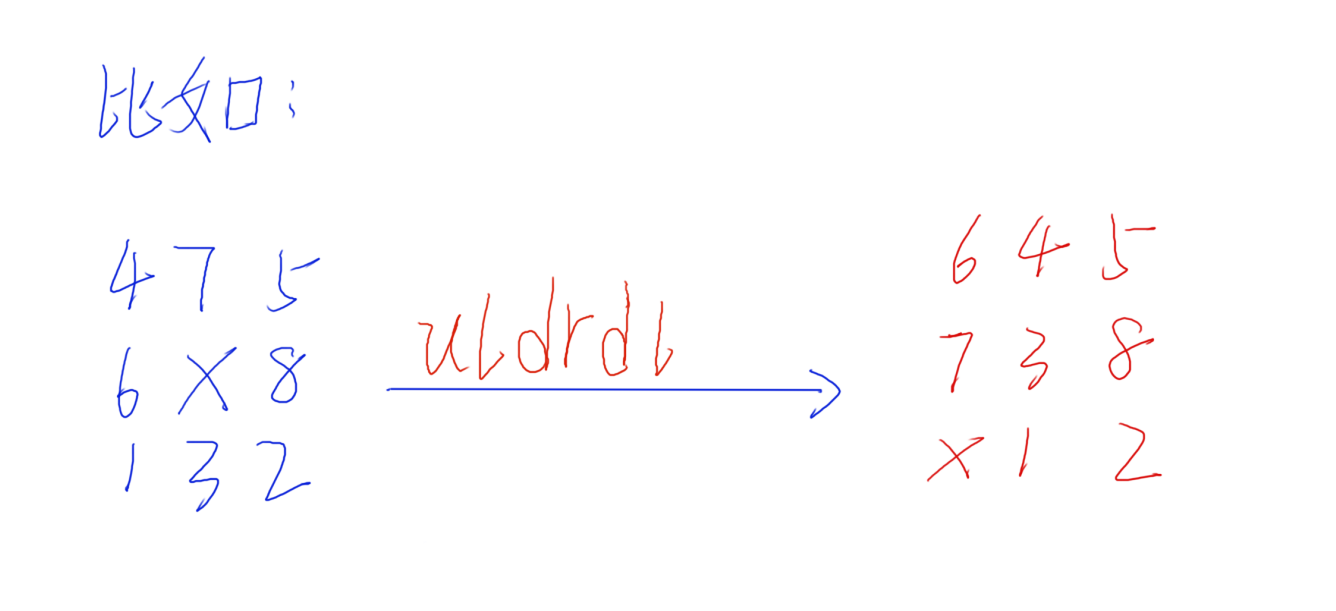
17、对于上面的初始状态，我们通过 uldrdl 这一连串操作变到后面的状态，如果我们要把它变回来，则需要进行的操作是：rulurd

18、这里为什么要提醒大家呢？因为很多人会觉得我们如何过来的那就如何回去就好了，但是事实并非如此，这里希望大家注意一下。上面的变换实际上是把每一个操作都取反向操作，然后倒过来操作就好了。（因为方向还是反的，本来是从终点到中间状态，而我们现在需要从中间状态到终点）

19、好了，具体代码的实现我们就大概说到这里。因为描述比较抽象，如果有不懂的地方建议结合代码一起看，会好很多。

20、另外，代码里面也有很多详细的注释，帮助大家好好理解每一步。

算法讲解视频

一、算法思路分析视频链接 : 八数码算法思路分析

二、算法代码落实视频链接 ：八数码代码落实详解

这题目的代码看起来很长，但是其实一点也不复杂，因为重复度比较高，很好理解的！

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<unordered_map>//用于哈希操作
#include<queue>

#define x first
#define y second

#define outt  cout<<t<<endl;
#define debug cout<<"这里没问题！"<<endl;
#define outkk  cout<<"kk "<<kk<<endl;

using namespace std;

typedef pair<char,string>PII;

//apre记录从起来出来的路径和转化方式
unordered_map<string,PII>apre,bpre;

//da 表示从起点出来的字符串到起点的距离 db表示从终点出来的距离终点的距离
unordered_map<string,int>da,db;

string kk="nul";

const int N=5;

//两个队列，分别用于存放从起点走出来的字符串和从终点走出来的字符串
queue<string>qa,qb;

char g[N][N];

/*--------------------------------------------------------------------------------------------------------------------*/
void set(string state)//这个函数是将我们当前的字符串转换为字符数组以便于我们进行变化操作
{
    for(int i=0;i<3;i++)g[0][i]=state[i];
    for(int i=3,j=0;i<6;i++,j++)g[1][j]=state[i];
    for(int i=6,j=0;i<9;i++,j++)g[2][j]=state[i];

}

string get()//这个是将我们变化后的数组转回字符串进行后续操作
{
    string res;

    for(int i=0;i<3;i++)
      for(int j=0;j<3;j++)
      res+=g[i][j];

    return res;
}

string change1(string state)//第一种变化方式 u
{
    set(state);//先把字符串转化为数组便于操作

    int xx,yx;//用于记录当前x的位置

    for(int i=0;i<3;i++)
      for(int j=0;j<3;j++)
       if(g[i][j]=='x'&&i==0)
       {
       return "x";//如果在边界上，说明不能走，返回 x 表示不能走
       }
       else if(g[i][j]=='x'&&i!=0)
       {
           xx=i;//如果可以走得话，记录一下下标，然后操作
           yx=j;
       }

    swap(g[xx][yx],g[xx-1][yx]);

    return get();//返回操作后的字符串
}
string change2(string state)//第二种变化方式 d
{
    set(state);//先把字符串转化为数组便于操作

    int xx,yx;//用于记录当前x的位置

    for(int i=0;i<3;i++)
      for(int j=0;j<3;j++)
       if(g[i][j]=='x'&&i==2)
       {
       return "x";//如果在边界上，说明不能走，返回 x 表示不能走
       }
       else if(g[i][j]=='x'&&i!=2)
       {
           xx=i;//如果可以走得话，记录一下下标，然后操作
           yx=j;
       }


    swap(g[xx][yx],g[xx+1][yx]);

    return get();//返回操作后的字符串
}
string change3(string state)//第三种变化方式 l
{
    set(state);//先把字符串转化为数组便于操作

    int xx,yx;//用于记录当前x的位置

    for(int i=0;i<3;i++)
      for(int j=0;j<3;j++)
       if(g[i][j]=='x'&&j==0)
       {
       return "x";//如果在边界上，说明不能走，返回 x 表示不能走
       }
       else if(g[i][j]=='x'&&j!=0)
       {
           xx=i;//如果可以走得话，记录一下下标，然后操作
           yx=j;
       }


    swap(g[xx][yx],g[xx][yx-1]);

    return get();//返回操作后的字符串
}

string change4(string state)//第四种变化方式 r
{
    set(state);//先把字符串转化为数组便于操作

    int xx,yx;//用于记录当前x的位置

    for(int i=0;i<3;i++)
      for(int j=0;j<3;j++)
       if(g[i][j]=='x'&&j==2)
       {
       return "x";//如果在边界上，说明不能走，返回 x 表示不能走
       }
       else if(g[i][j]=='x'&&j!=2)
       {
           xx=i;//如果可以走得话，记录一下下标，然后操作
           yx=j;
       }


    swap(g[xx][yx],g[xx][yx+1]);

    return get();//返回操作后的字符串
}
/*--------------------------------------------------------------------------------------------------------------------*/

//上面全是操作函数，大家可以稍微看一下
int num=0;

int extrend(queue<string>&q,int tt)//扩展一下队内元素较少的那一个，能有效减少我们的算法实际运行效率
{
    for(int i=0;i<q.size();i++)
    {
        string t=q.front();//取出对头扩展

        q.pop();//出队

        string state4[5];//记录一下我们不同操作对应的结果状态

        int is[5]={};//用于操作是否合法（比如，我们如果在最右边那么我们就不能和右边的交换）

        if(change1(t)!="x")//如果说能走，那就赋值
        state4[1]=change1(t);
        else
        is[1]=1;//如果不能走就标记一下
        if(change2(t)!="x")
        state4[2]=change2(t);
        else
        is[2]=1;
        if(change3(t)!="x")
        state4[3]=change3(t);
        else
        is[3]=1;
        if(change4(t)!="x")
        state4[4]=change4(t);
        else
        is[4]=1;

        if(!tt)//判断一下当前扩展的是队列a还是队列b

        {
          for(int i=1;i<=4;i++)
          if(!da[state4[i]]&&!is[i])
          {
              da[state4[i]]=da[t]+1;

                if(i==1)
                 apre[state4[i]]={'u',t};//存一下当前用了哪一个操作，还有当前是从哪一个字符串转移过来的
               else if(i==2)
                 apre[state4[i]]={'d',t};
               else if(i==3)
                 apre[state4[i]]={'l',t};
               else
                 apre[state4[i]]={'r',t};
             //如果当前的字符串在对方中已经被找到过了，那说明二者之间已经有了一个联系，那就可以结束寻找了
             if(db[state4[i]]!=0)//如果对方已经搜到了
             {
                 kk=state4[i];
                 return db[state4[i]];
             }

              q.push(state4[i]);//放入队列进行扩展
          }

        }
        else//判断一下当前扩展的是队列a还是队列b
        {
          for(int i=1;i<=4;i++)
          if(!db[state4[i]]&&!is[i])
          {
              db[state4[i]]=db[t]+1;

                if(i==1)
                 bpre[state4[i]]={'u',t};//存一下当前用了哪一个操作，还有当前是从哪一个字符串转移过来的 
               else if(i==2)
                 bpre[state4[i]]={'d',t};
               else if(i==3)
                 bpre[state4[i]]={'l',t};
               else
                 bpre[state4[i]]={'r',t};
             //如果当前的字符串在对方中已经被找到过了，那说明二者之间已经有了一个联系，那就可以结束寻找了
             if(da[state4[i]]!=0)
             {
                 kk=state4[i];//先记录一下中间连接串是哪一个，方便后续找出路径   (需要说明)
                 return da[state4[i]];
             }

              q.push(state4[i]);//放入队列进行扩展
           }
        }

    }

    return -1;//如果本次扩展没有找到连接前后的字符串，那就返回-1表示还需要继续找
}

int bfs(string A,string B)
{
    qa.push(A);//先将起点放入我们从起点开始扩展的队列，作为起点

    da[A]=0;//让起点距离起点的距离设置为0

    qb.push(B);//先将终点放入我们从终点开始扩展的队列，作为终点

    db[B]=0;//让终点距离终点的距离设置为0

    while(qa.size()&&qb.size())//当二者队列里面同时含有元素的时候，才满足继续扩展的条件  (需要说明)
    {
  //神奇的特判操作，由于这题目的特殊性质，双方有可能搜了很久还是没搜到交集，那么就其实说明无解了  (需要说明)
        if(num>=10000)return -1;


        int t,tt;//tt用于判断我们当前是该扩展 a 还是扩展 b
        if(qa.size()<=qb.size())
        {
            tt=0;
             t=extrend(qa,tt);

             num+=qa.size();
        }

        else
        {
            tt=1;
            t=extrend(qb,tt);
            num+=qb.size();
        }

        if(t!=-1)
        return t;
    }

    return -1;//如果到最后都没有找到的话，那也说明无解了
}

int main()
{
    string A,B;

    for(int i=1;i<=9;i++)
    {
        B+=char(i+'0');//生成一下我们的终点
        char x;

        scanf(" %c",&x);

        A+=x;//生成起点
    }
    B[8]='x';//生成终点

      int ans=bfs(A,B);//然后直接进行搜索


     string res1,res2;

     if(ans==-1)//如果返回的是-1 那说明无解
     printf("unsolvable");
     else//如果有解
     {
      string tt=kk; //首先我们要找到连接二者的中介，也就是我们记录下来的中介
      while(tt!=A)//找出我们从起点到中间点所经历的操作
      {
          res1+=apre[tt].x;
          tt=apre[tt].y;
      }
      //由于我们所得到的顺序是从中间到起点的，那么我们需要的是从起点到中间的，直接倒一边就好了
      //注意这里只是顺序反了一下，操作是没问题的，因为我们实际上就是从起点到终点的
      //只不过我们取出来的时候是反向取的，和下面的操作有一些差别
      reverse(res1.begin(),res1.end());
      tt=kk;
      /*这一步操作需要特殊说明，由于我们实际上，也就是代码上实现的是从终点到中间点的，但是我们需要的是
      从中间点到终点的，它的转换其实不是一个简单的倒回去操作就可以实现的，比如，我们在前面解释过的例子
      我们需要把每个操作都反一下，才是回来的操作，也就是从中间点到终点的操作(前面已经解释)
      */
      while(tt!=B)
      {
          char aa=bpre[tt].x;

          if(aa=='u'||aa=='d')
          aa='u'+'d'-aa;//回去的时候要转化
          else
          aa='l'+'r'-aa;//回去的时候要转化
          res2+=aa;
          tt=bpre[tt].y;
      }
   //为什么后半段不需要转化呢？前面已经解释过了就不再赘述

      cout<<res1<<res2;//最后输出两段合起来的就好了
     }

/*---------------------------------------------------------------------------------------------------------------------*/
    //  string zheng="ullddrurdllurrdlurd";

    // for(int i=0;i<zheng.size();i++)
    // {
    //     if(zheng[i]=='u')
    //     {
    //         set(A);

    //         A=change1(A);
    //     }
    //     else if(zheng[i]=='d')
    //     {
    //          set(A);
    //         A=change2(A);
    //     }
    //     else if(zheng[i]=='l')
    //     {
    //          set(A);
    //         A=change3(A);
    //     }
    //     else
    //     {
    //          set(A);
    //         A=change4(A);
    //     }
    // }

    // cout<<kk<<endl;
    // cout<<A<<endl;
    // 1237486x5

    // uldldrrulldrrulu ruulddlurdrulul
/*----------------------------------------------------------------------------------------------------------------------*/
//这上面是debug用的代码，为了验证一下程序的正确性，还有找一下问题的产生点
    return 0;
}

码字不易，点个赞再走呗~~