题目描述

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。
给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

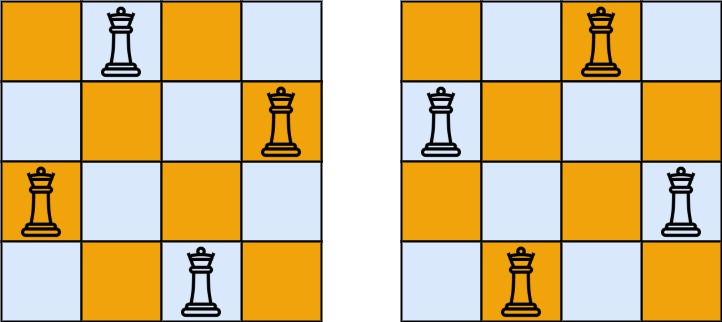
示例 1：
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：
输入：n = 1
输出：[["Q"]]
 

提示：
1 <= n <= 9
皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上。

算法1

暴力遍历 逐步尝试每行每个点能否放置棋子

检测是否有冲突的时候注意规律如下

1 横竖行是否有冲突 检测的是x或者y分别不懂 另一坐标变化

例如 board[1][0] board[1][1] board[1][2] board[1][3] board[1][4]

board[0][1] board[1][1] board[2][1] board[3][1] board[4][1]

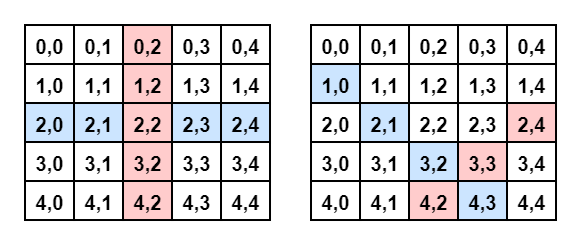
2 检测斜行是否有冲突，观察到规律

斜行的坐标要么差值相同 要么和相同

比如 board[1][0] board[2][1] board[3][2] 差值相同

board[1][3] board[2][2] board[3][1] 和值相同

C++ 代码

class Solution {
public:
    vector<vector<string>> ans;
    vector<string> board;

    bool Check(int x,int y){
        //检测 横竖 斜行 有无冲突
        for(int i = 0;i < board.size();i++){
            for(int j = 0;j<board.size();j++){
                if( ((i+j) == (x+y) && board[i][j] =='Q') || 
                   ( (i-j) ==(x-y) &&  board[i][j] =='Q') )
                {
                    return false;
                }
            }
        }

        for(int i = 0; i < board.size();i++){
            if(board[x][i] =='Q' || board[i][y] == 'Q') {return false;}
        }

        return true;
    }

    void dfs(int idx){
        if(idx ==board.size()){
            ans.push_back(board);
            return ;
        }

        for(int i = 0; i < board.size() ; i++){
            if(Check(idx,i) == true){
                board[idx][i] = 'Q';
                dfs(idx+1);
                board[idx][i] = '.';
            }
        }
    }

    vector<vector<string>> solveNQueens(int n) {
        board = vector<string> (n,string(n,'.'));
        dfs(0);
        return ans;
    }
};

我的视频题解空间