剑指 Offer 11. 旋转数组的最小数字

博客地址

题目链接：

AcWing 22. 旋转数组的最小数字
LeetCode 剑指 Offer 11. 旋转数组的最小数字

思路：

参考题解：
旋转数组的最小数字

面试题11. 旋转数组的最小数字（二分法，清晰图解）

没有重复数字的情况：

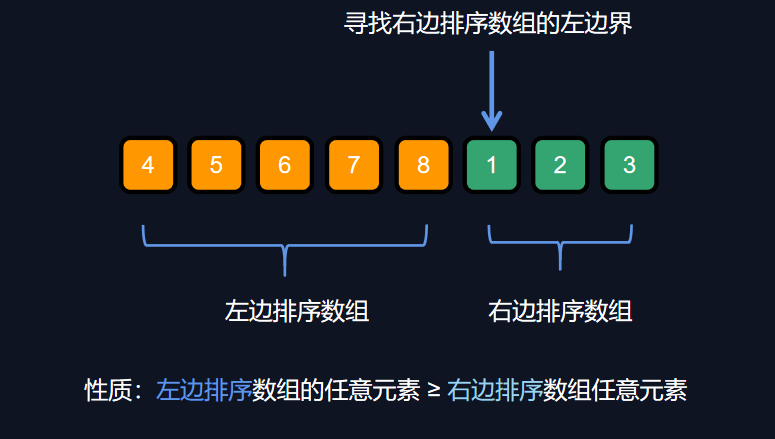
算法模板不变，check函数比较复杂

根据性质可以得出

if(numbers[mid] > numbers[r])l = mid + 1;
else if(numbers[mid] < numbers[r] ) r = mid;

但是当numbers[mid] == numbers[r]的时候很难判断旋转点x（右边排序数组的左边界）在哪个区间里面

有重复数字的情况

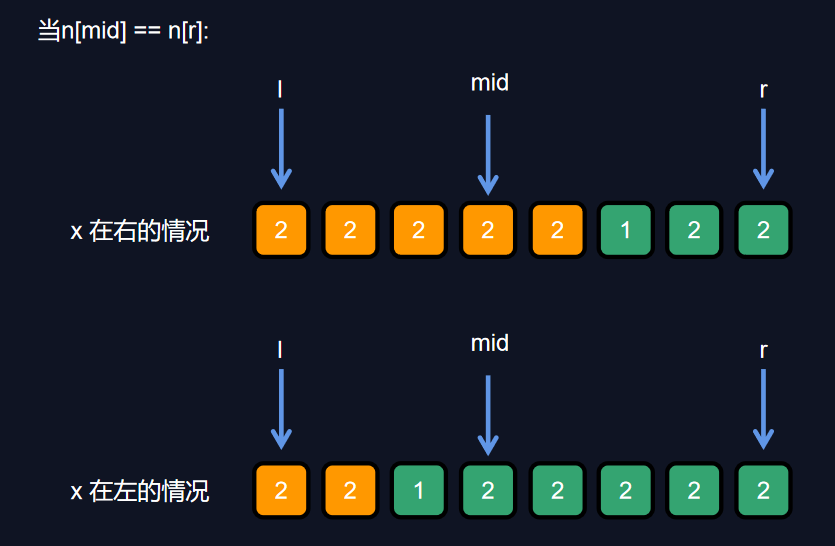
我们很难以上条件进行判断，那么我们可以暴力的让right指针向左移动 r --，依次来减小搜索范围。

但是我们并不知道旋转点倒是在左右哪个区间，因此不能随便的忽略一部分值。

但是由numbers[mid] == numbers[r] 可以知道他们的值是相等的，就算我们忽略掉的这个值刚好是旋转点，我们也有一个替代品。

因此我们忽略二分区间的右边界点进行r --

因为x = r又因为 numbers[r] = numbers[mid] 所以numbers[mid] = numbers[r] = numbers[x]

又因为是递增，且x是旋转点 所以numbers[x]是整个二分区间的最小值。

而x到i到mid是递增的，可 numbers[x] = numbers[mid] 所以当r--之后，[l,x]的值等于numbers[x]

而[mid,r]之间值，是>= numbers[x]的，所以经过二分之后，区间会选择在左边的区间[l,x]

以上可得，[l,x]都是等于number[x]所以，最后的结果依旧是旋转点。

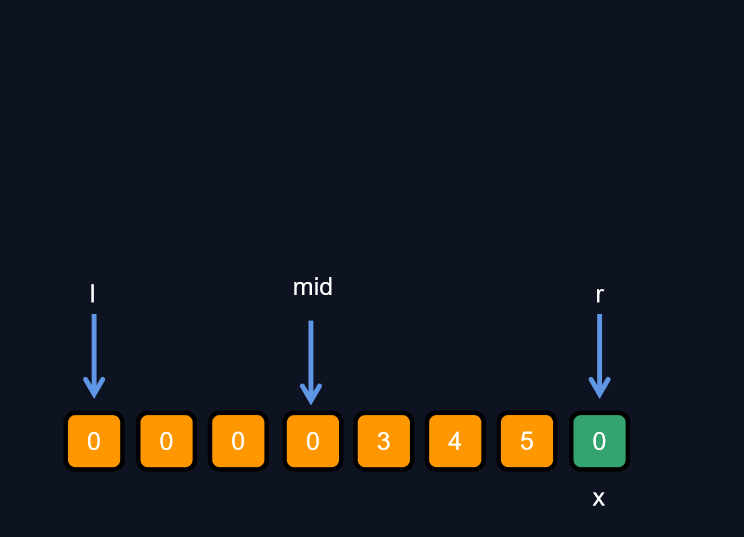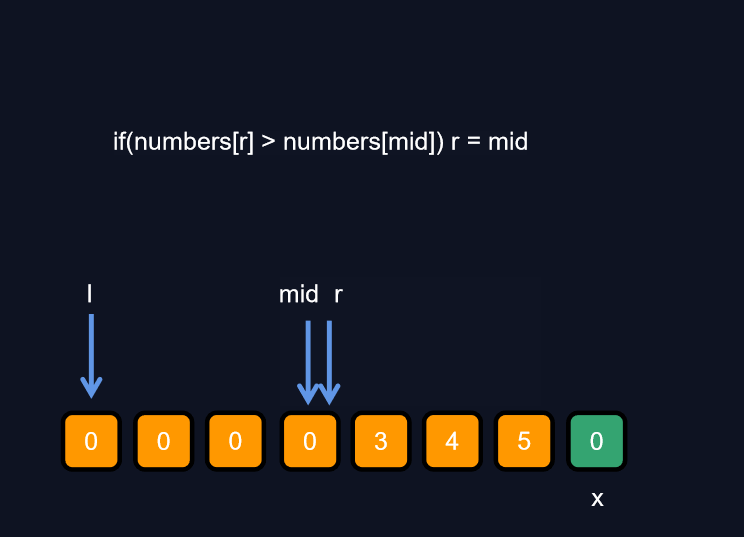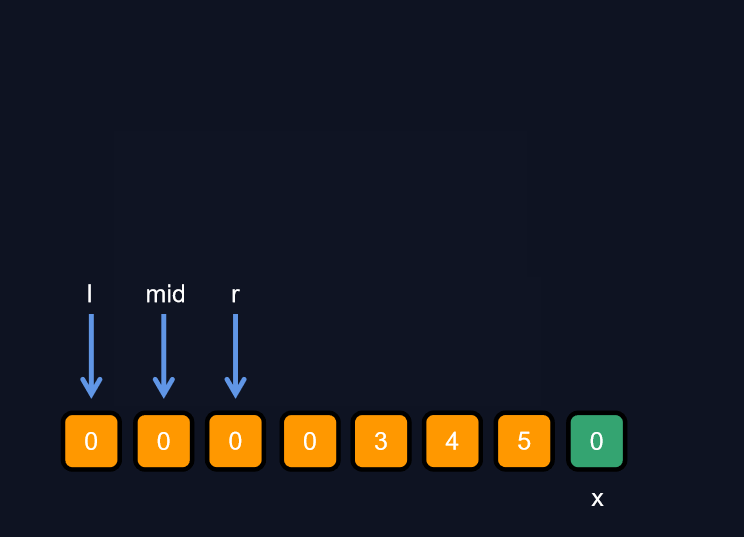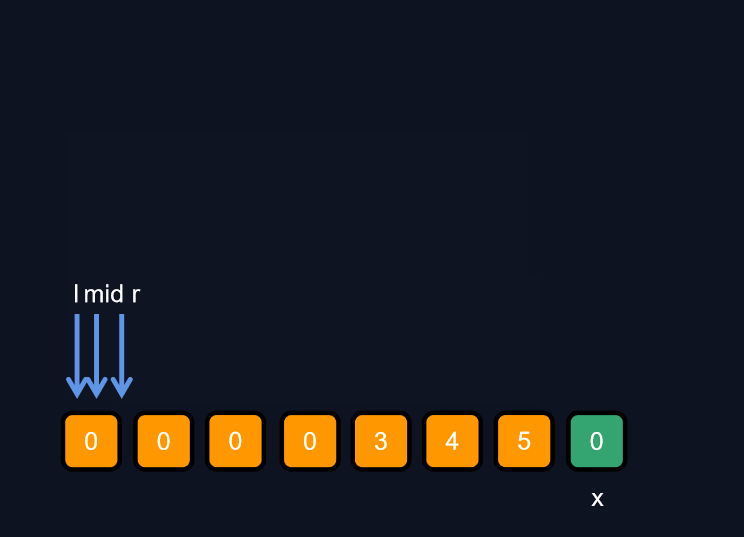
代码：

class Solution {
public:
    int minArray(vector<int>& numbers) {
        int l = 0, r = numbers.size()-1;

        while(l < r){
            int mid = l + r >> 1;
            if(numbers[mid] > numbers[r])l = mid + 1;
            else if(numbers[mid] < numbers[r] ) r = mid;
            else r --;
        }
        return numbers[l];
    }
};