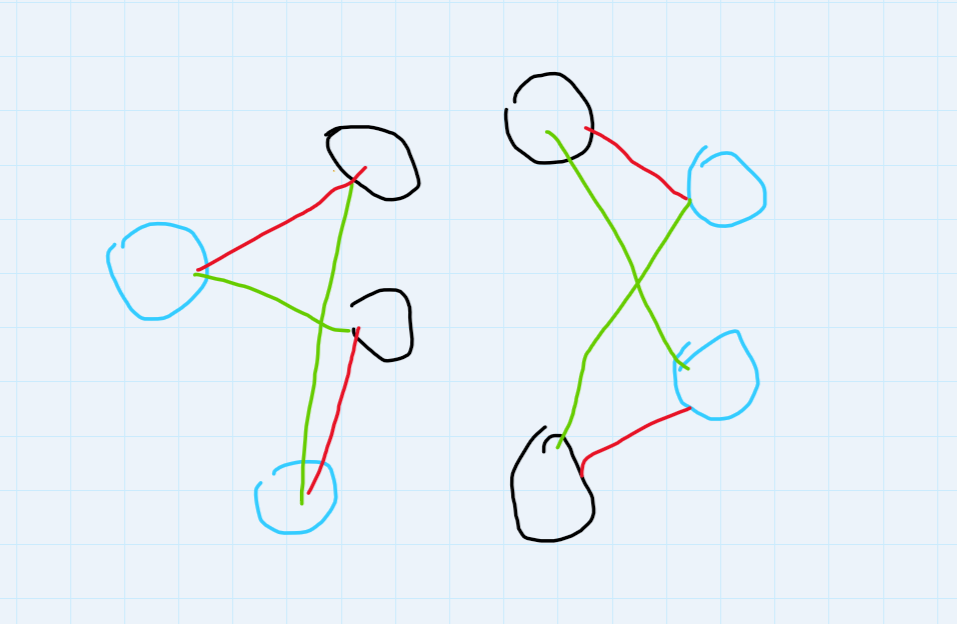
所有点之间的距离和最短一定满足题意，即将每个点之间的距离作为费用，最小费用流即为可行方案
对于每两对点相连，用三角形两边之和大于第三边可证明交叉边(绿边）一定大于不交叉边（红边）

算法1

(最小费用流)

C++ 代码

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<ctime>
#include<cmath>
#include<string>
#include<cstring>
#include<bitset> 
#include<vector>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<iomanip>
#include<algorithm>
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define endl "\n"
#define int long long
#define PI  acos(-1)
//CLOCKS_PER_SEC clock()函数每秒执行次数
using namespace std;

const int INF = 0x3f3f3f3f;
const int N = 205,M = N * N * 2;
int mod = 1e9 +7;
int n,m,k,S,T;
int e[M],ne[M],f[M],h[N],idx;
double w[M];
void add(int a,int b,int c,double d){
    e[idx] = b,f[idx] = c,w[idx] = d,ne[idx] = h[a],h[a] = idx++;
    e[idx] = a,f[idx] = 0,w[idx] =-d,ne[idx] = h[b],h[b] = idx++;
}
struct node{
    int x,y;
}a[N];
double get_dis(node a,node b){
    double dx = a.x - b.x;
    double dy = a.y - b.y;
    return sqrt(dx * dx + dy * dy);
} 
int ans[N];
int incf[N],pre[N];
bool vis[N];
double d[N];
bool spfa(){
    queue<int> q;
    fill(d,d + 2 * n + 2,1e18);
    memset(vis,false,sizeof(vis));
    memset(incf,0,sizeof(incf));
    q.push(S);
    d[S] = 0,incf[S] = INF;
    while(!q.empty()){
        int u = q.front();q.pop();
        vis[u] = false;
        for(int i = h[u] ; ~i ; i = ne[i]){
            int ver = e[i];
            if(f[i] && d[ver] > d[u] + w[i]){
                d[ver] = d[u] + w[i];
                incf[ver] = min(incf[u],f[i]);
                pre[ver] = i;
                if(!vis[ver]){
                    q.push(ver);
                    vis[ver] = true;
                }
            }
        }
    }
    return incf[T] > 0;
}
void EK(){
    while(spfa()){
        int t = incf[T];
        for(int i = T ; i != S ; i = e[pre[i] ^ 1]){
            f[pre[i]] -= t,f[pre[i] ^ 1] += t;
        }
    }
}
void solve(){
    cin >> n;
    S = 0,T = 2 * n + 1;
    memset(h,-1,sizeof(h));
    for(int i = 1 ; i <= n ; ++i){
        cin >> a[i].x >> a[i].y;
        //从源点向所有黑点（二分图左部）连容量为1费用为0的边 
        add(S,i,1,0);
    }
    for(int i = 1 ; i <= n ; ++i){
        cin >> a[i + n].x >> a[i + n].y;
        //从所有白点（二分图右部）向汇点连容量为1费用为0的边 
        add(i + n,T,1,0);
    }
    for(int i = 1 ; i <= n ; ++i){
        for(int j = 1 ; j <= n ; ++j){
            //从左部点向右部点连容量为1费用为距离的边 
            add(i,j + n,1,get_dis(a[i],a[j + n]));
        }
    }
    EK();
    for(int i = 1 ; i <= n ; ++i){
        for(int j = h[i] ; ~j ; j = ne[j]){
            //残留网络中流量为0表示选择了该边 
            if(f[j] == 0){
                cout << e[j] - n << endl; 
                break;
            }
        }
    }
}

signed main(){
    IOS;
    solve();
    return 0;
}