题目描述

给你一个由正整数组成的数组 nums。

数字序列的 最大公约数 定义为序列中所有整数的共有约数中的最大整数。

例如，序列 [4,6,16] 的最大公约数是 2。
数组的一个 子序列 本质是一个序列，可以通过删除数组中的某些元素（或者不删除）得到。

例如，[2,5,10] 是 [1,2,1,2,4,1,5,10] 的一个子序列。
计算并返回 nums 的所有 非空 子序列中 不同 最大公约数的 数目。

样例

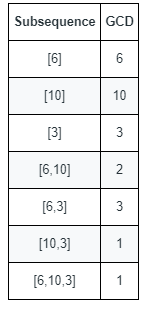
输入：nums = [6,10,3]
输出：5
解释：上图显示了所有的非空子序列与各自的最大公约数。
不同的最大公约数为 6 、10 、3 、2 和 1。

输入：nums = [5,15,40,5,6]
输出：7

限制

• 1 <= nums.length <= 10^5
• 1 <= nums[i] <= 2 * 10^5

算法

(暴力枚举) $O(n + m \log^2 m)$

1. 使用一个布尔数组记录数字是否出现过。假设 $m$ 为出现过的最大的数字。
2. 从 1 开始枚举约数直到 $m$。对于每个约数 $i$，如果所有是 $i$ 的倍数的数字的最大公约数为 $i$，则 $i$ 必定是这些数字构成的子序列的最大公约数。

时间复杂度

• 初始化数字是否出现过需要 $O(n + m)$ 的时间。
• 枚举的时间最多为 $m + m / 2 + m / 3 + … + 1 = O(m \log m)$，求最大公约数的时间复杂度为 $O(\log m)$。
• 故总时间复杂度为 $O(n + m \log^2 m)$。

空间复杂度

• 需要 $O(m)$ 的额外空间存储数字是否被使用。

C++ 代码

class Solution {
public:
    int countDifferentSubsequenceGCDs(vector<int>& nums) {
        const int M = 200000;
        vector<bool> seen(M + 1, false);
        int m = 0;
        for (int x : nums) {
            seen[x] = true;
            if (m < x) m = x;
        }

        int ans = 0;
        for (int i = 1; i <= m; i++) {
            int g = 0;
            for (int j = i; j <= m && g != i; j += i)
                if (seen[j])
                    g = __gcd(g, j);

            if (g == i)
                ans++;
        }

        return ans;
    }
};