知识梗概

Bellman-Ford算法

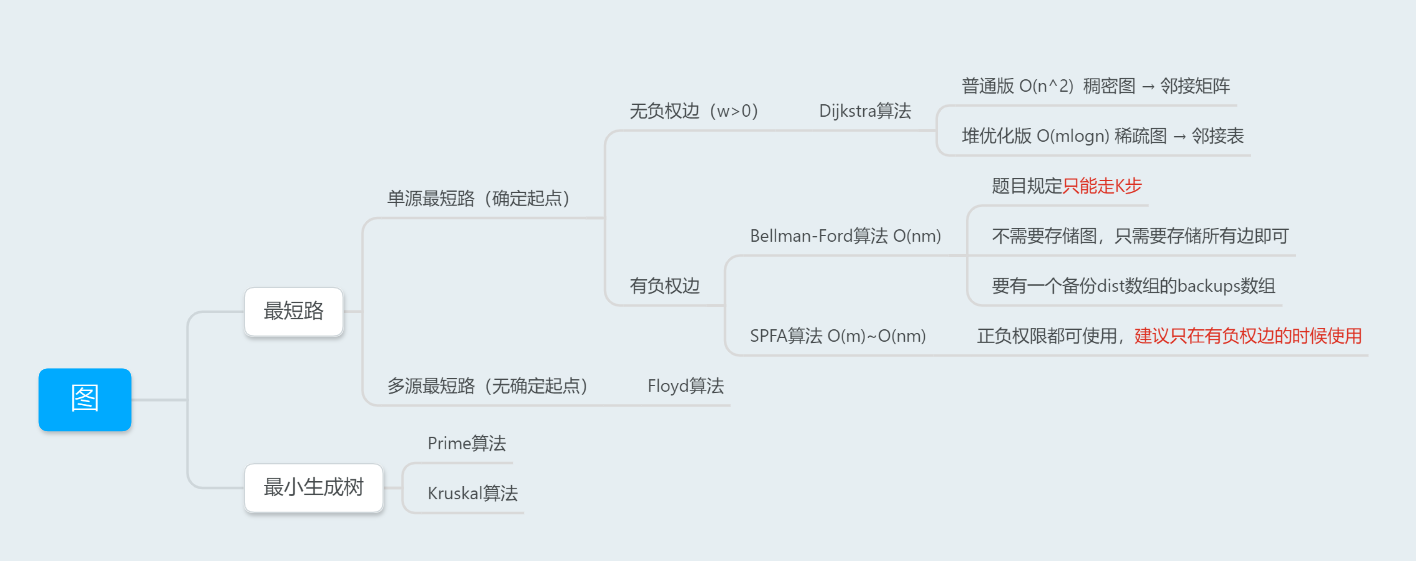
特征

1.题目规定只能走K步（有步数限制），存在负权边
2.不需要存储图，只需要存储所有边即可
3.要有一个备份dist数组的backups数组

模板流程

//dist[N]:距离数组  bak[N]:备份数组  k:题设规定步数
int dist[N],bak[N],k;

//结构体数组用于存储边，含义：a到b距离为c
struct N{
    int a,b,c;
}Ns[10010];


//初始化dist数组，并设定起点距离为0

//最多走k步，循环k次
for(k次){
    //将dist数组进行备份

    //遍历所有边，进行更新(用备份数组更新距离数组)
    for(...){
        if(dist[b]>backups[a]+w) dist[b]=backups[a]+w;
    }

    //注意不可达情况的判别:由于在更新过程中可能会对0x3f3f3f3f进行少量的加减，所以取中值进行判断
    if(dist[n]>0x3f3f3f3f/2) return -1;
    return dist[n];

}

题解

#include<iostream>
#include<cstring>
using namespace std;

int dist[550],bak[550],n,m,k;

//开一个结构体数组用于存储边，含义：a到b距离为c
struct N{
    int a,b,c;
}Ns[10010];


void bellman_ford(){
    memset(dist,0x3f3f3f3f,sizeof dist);
    dist[1]=0;

    for(int i=0;i<k;i++){
        memcpy(bak,dist,sizeof dist); //拷贝备份数组
        for(int j=0;j<m;j++){
            int a=Ns[j].a,b=Ns[j].b,c=Ns[j].c;
            if(dist[b]>bak[a]+c) dist[b]=bak[a]+c;

        }

    }
    if(dist[n]>0x3f3f3f3f/2) cout<<"impossible";
    else cout<<dist[n];
}
int main(){
    cin>>n>>m>>k;
    for(int i=0;i<m;i++){
        int a,b,c;
        cin>>a>>b>>c;
        Ns[i]={a,b,c};
    }
    bellman_ford();

    return 0;
}

⭐⭐
重要代码
memcpy(bak,dist,sizeof dist); //拷贝备份数组