题目描述

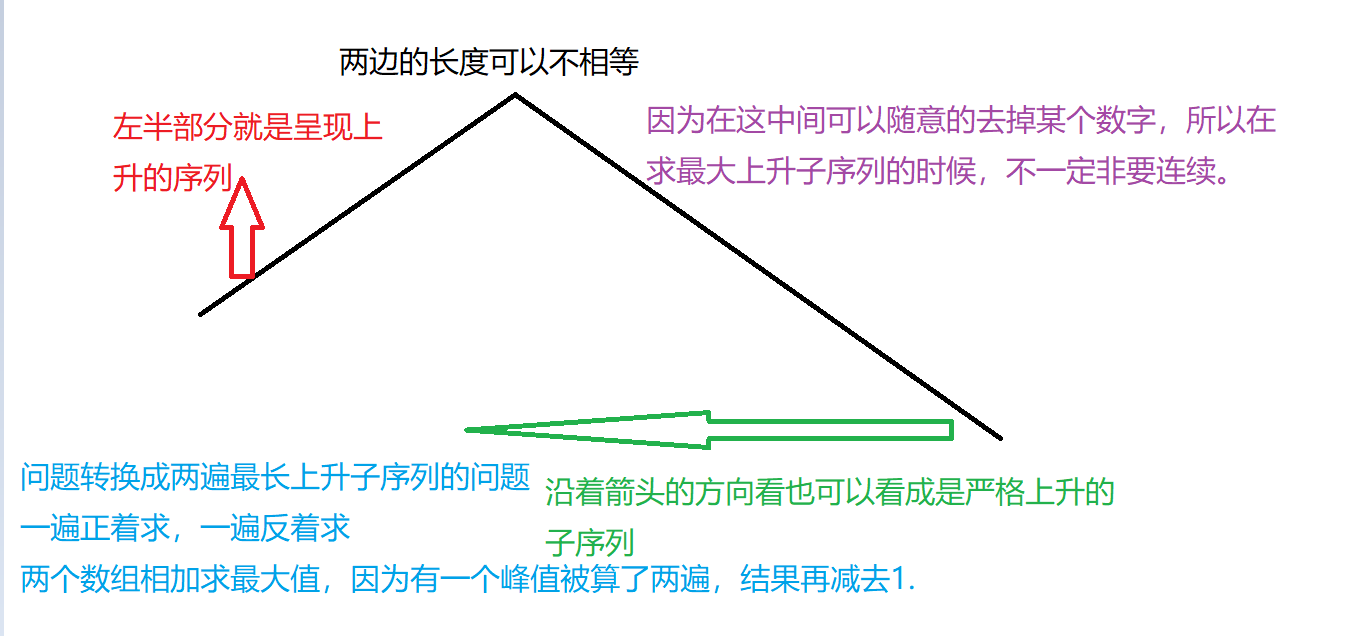
题目的主要含义就是说，你需要找到一个序列使得序列中的元素呈现出先上升后下降的走势的最大长度
总长度减去最大长度就是结果

本题相关

最长上升子序列
最长上升子序列 II 优化思想：贪心+二分

算法思想

看了这个题目的算法标签，想了好久终于想出来了做法

注意的地方

在反向求最大上升子序列问题的时候需要注意j>i,i是指的每一个元素，j是指在i后面的元素，和i后面的元素依次比较
也就是求以i开头的最长的上升子序列问题

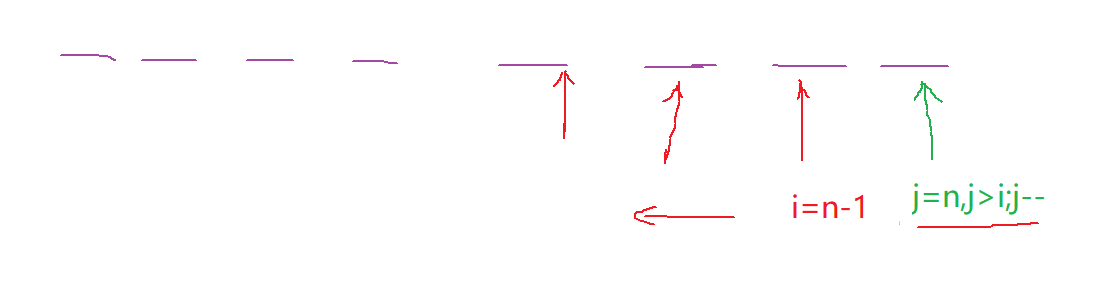
也可以理解成最长降序子序列的长度

package day;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;

public class 合唱队形 {

    /**
     * @param args
     * @throws IOException 
     * @throws NumberFormatException 
     */
    public static void main(String[] args) throws NumberFormatException, IOException {
        // TODO Auto-generated method stub
    BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
    int n=Integer.parseInt(bufferedReader.readLine());
    int a[]=new int [n+1];
    String p[]=bufferedReader.readLine().split(" ");
    for(int i=1;i<=n;i++){
        a[i]=Integer.parseInt(p[i-1]);
    }
    int f[]=new int [n+1];
    Arrays.fill(f, 1);
    int f1[]=new int [n+1];
    Arrays.fill(f1, 0);

    for(int i=2;i<=n;i++){

        for(int j=1;j<i;j++){
            if(a[i]>a[j]){
                f[i]=Math.max(f[i], f[j]+1);
            }
        }
    }

    for(int i=n-1;i>=1;i--){
        for(int j=n;j>i;j--){
            if(a[i] > a[j]){
                f1[i]=Math.max(f1[i], f1[j]+1);
            }
        }
    }

    int ma=0;
    for(int i=1;i<=n;i++){
        f[i]+=f1[i];
        ma=Math.max(ma, f[i]);
    }
    System.out.println(n-ma);

    }

}