分析

• 对于每一个车次，都会在某个连续的区间运行，在这个区间内部（包含端点）有些车站会停车（这些车站的集合记为A），有些车站不会停车（这些车站的集合记为B），则A中所有元素的级别都严格大于B中车站的级别，即$a_i \ge b_i + 1$，$a_i \in A, b_i \in B$，另外还有$a_i \ge 1$，可以看出这是一个差分约束问题。

• 于是问题变为了让我们求解在满足上述两个不等式的条件下，在所有可能的车站编号方式（可能存在多种编号方式），对于每种编号方式里的所有车站编号都会存在一个最大值，在这些最大值中找到最小的那一个。

• 对于每一个车次，根据不等式，我们可以从$b_i$向$a_i$连一条边权为1的边。对于所有的车次都这样操作，我们就可以得到一个图。在这个图上求最长路即可，此时我们会得到一种最优的编号方式，即会得到每个车次的最小编号，取最大的那一个即可。

• 至此，这一题本质上就是AcWing 1192. 奖金这道题，但是问题有那么简单吗？答案是问题没有那么简单。

• 我们考虑需要建立多少条边，最多存在1000个车站，最多有1000个车次，最坏情况下对于每个车次我们需要建立$500 \times 500 = 2.5 \times 10 ^ 5$条边，因此1000个车次需要建立$2.5 \times 10^8$条边，这对于内存以及时间都是不可接受的，因此我们需要优化这一题的建边方式。

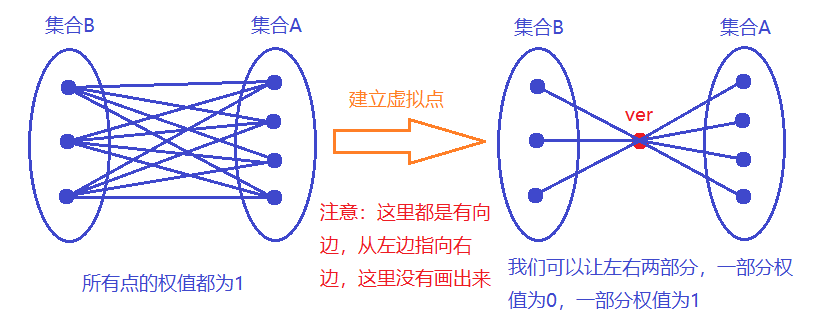
• 对于每个车次，我们不直接让集合B中所有的点连向集合A中所有的点，而是在两者之间建立一个虚拟源点，这样$500 \times 500$就可以变成$500+500$了，这样时间和空间都可以接收了，如下示意图：

• 在这个新图上求最长路即可。注意，假设图中有n个点，我们用1~n表示原来的点，代码实现中，使用n+i表示第i个虚拟源点（i从1开始）。

• 和AcWing 1192. 奖金这道题类似，递推的过程中我们并不需要在代码中显示的建立超级源点（根据$a_i \ge 1$可以建立超级源点），因为有解的话图一定是DAG，可以将所有点的初始距离初始化为100，然后递推求解即可。

• 考虑点数和边数的最大值，因为每个车次都要建议一个虚拟源点（注意和超级源点的区别），因此点数最多为2000；每个车次最多建立1000条边，因此最多建立一百万条边。

#include <iostream>
#include <cstring>

using namespace std;

const int N = 2010, M = 1000010;

int n, m;  // n个火车站, m个车次
int h[N], e[M], w[M], ne[M],idx;
int q[N];  // 拓扑排序使用的队列
int d[N];  // 每个点的入度
int dist[N];  // 每个点距离超级源点的最长距离
bool st[N];  // 记录每个车次中哪些车站需要停车

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
    d[b]++;  // b的入度加1
}

void topsort() {

    int hh = 0, tt = -1;
    for (int i = 1; i <= n + m; i++)
        if (!d[i])
            q[++tt] = i;

    while (hh <= tt) {
        int t = q[hh++];
        for (int i = h[t]; ~i; i = ne[i]) {
            int j = e[i];
            if (--d[j] == 0)
                q[++tt] = j;
        }
    }
}

int main() {

    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);

    for (int i = 1; i <= m; i++) {

        memset(st, 0, sizeof st);
        int cnt;  // 当前车次经停的车站数量
        scanf("%d", &cnt);
        int start = n, end = 1;  // 起始站和终点站
        while (cnt--) {
            int stop;
            scanf("%d", &stop);
            start = min(start, stop);
            end = max(end, stop);
            st[stop] = true;
        }

        int ver = n + i;  // 虚拟源点
        for (int j = start; j <= end; j++)
            if (!st[j]) add(j, ver, 0);  // 集合B向ver连一条权值为0的边, 可以参考上面的分析
            else add(ver, j, 1);  // 从ver向会停车的集合A连一条权值为1的边
    }

    topsort();

    // 递推求最长路
    for (int i = 1; i <= n; i++) dist[i] = 1;
    for (int i = 0; i < n + m; i++) {  // 拓扑序列在q[0]~q[n+m-1]中
        int j = q[i];
        for (int k = h[j]; ~k; k = ne[k])  // 边(j, e[k])
            dist[e[k]] = max(dist[e[k]], dist[j] + w[k]);
    }

    int res = 0;
    for (int i = 1; i <= n; i++) res = max(res, dist[i]);

    printf("%d\n", res);

    return 0;
}