分析

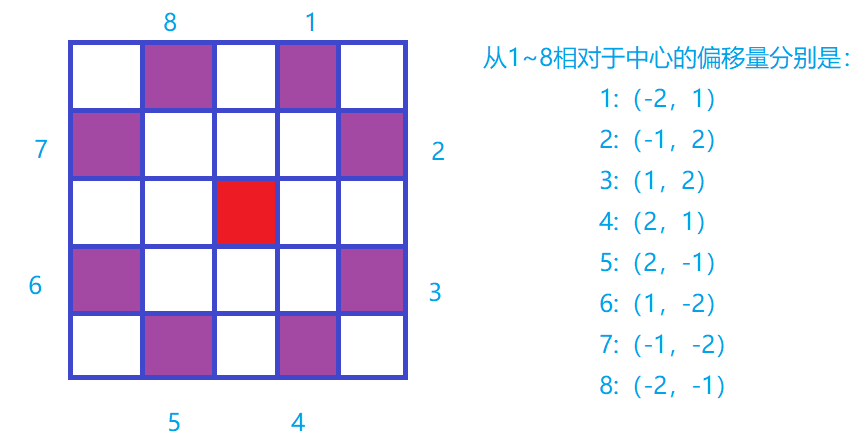
• 使用偏移量技巧，可以很方便的遍历8个方向

#include <iostream>
#include <cstring>

#define x first
#define y second

using namespace std;

typedef pair<int, int> PII;

const int N = 155, M = N * N;

int n, m;
char g[N][N];
PII q[M];
int dist[N][N];

int bfs() {

    int dx[] = {-2, -1, 1, 2, 2, 1, -1, -2};
    int dy[] = {1, 2, 2, 1, -1, -2, -2, -1};

    // 寻找起点
    int sx, sy;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < m; j++)
            if (g[i][j] == 'K') {
                sx = i, sy = j;
                break;
            }

    memset(dist, -1, sizeof dist);
    int hh = 0, tt = 0;
    q[0] = {sx, sy};
    dist[sx][sy] = 0;

    while (hh <= tt) {
        auto t = q[hh++];
        for (int i = 0; i < 8; i++) {
            int a = t.x + dx[i], b = t.y + dy[i];
            if (a >= 0 && a < n && b >= 0 && b < m && dist[a][b] == -1 && g[a][b] != '*') {
                if (g[a][b] == 'H') return dist[t.x][t.y] + 1;
                q[++tt] = {a, b};
                dist[a][b] = dist[t.x][t.y] + 1;
            }
        }
    }
    return -1;
}

int main() {

    cin >> m >> n;
    for (int i = 0; i < n; i++) cin >> g[i];

    cout << bfs() << endl;

    return 0;
}