• 此时仍然需要使用时间戳以及$dfn、low$数组。

• 首先我们需要考虑如何求割点？考虑DFS过程中从点x遍历到点y，如果有$low[y] \ge dfn[x]$，则：

① 如果x不是根节点，那么x是割点；

② 如果x是根节点，则至少存在两各个节点y，使得$low[y_i] \ge dfn[x]$，此时x才是割点。

分析

• 做法如下：

（1）统计一下所有连通块的个数（结果为cnt）；

（2）枚举从哪个块中删，然后再枚举这个块中删除哪个点，会得到删除点之后形成块的数量，去最大值，记为ans。最终的答案就是ans+cnt-1。

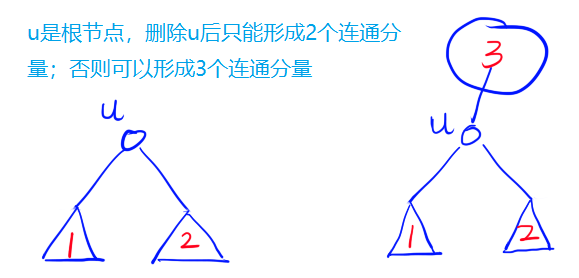
• 我们需要考虑删除哪个点？答案是我们应该删除每个连通块中的割点，因为根据割点定义，只有删除割点才能使连通块的数量增加。对于每个连通块而言，如果u是割点，假设u存在2个孩子，此时还需要判断u是否为这个图的根节点（即遍历该连通块时第一个遍历到的节点），如果是根节点，则删去u之后能形成2个连通块，如果u不是根节点，则删去u之后能形成3个连通块，如下图：

#include <iostream>
#include <cstring>

using namespace std;

const int N = 10010, M = 30010;

int n, m;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp;
int root;  // 记录每个连通块的"根节点"
int ans;  // 记录每个连通块去掉一个点形成的连通块数目的最大值

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void tarjan(int u) {

    dfn[u] = low[u] = ++ timestamp;

    int s = 0;  // 如果当前点u是割点的话，去掉该点u得到的连通分量的个数
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (!dfn[j]) {
            tarjan(j);
            low[u] = min(low[u], low[j]);
            if (dfn[u] <= low[j])  // 说明u是可能是割点, u存在一棵子树
                s++;
        } else low[u] = min(low[u], dfn[j]);
    }

    //如果不是根节点
    /*
             /
            u    删掉u后 除子节点yi外
           / \           还要要加上父节点部分+1
          o   o
    */
    if (u != root) s++;  // 不用加上&& s的判断,因为u不是割点的话,s要取1

    ans = max(ans, s);
}

int main() {

    while (scanf("%d%d", &n, &m), n || m) {

        memset(dfn, 0, sizeof dfn);  // dfn还具有判重数组的作用
        memset(h, -1, sizeof h);
        idx = timestamp = 0;

        while (m--) {
            int a, b;
            scanf("%d%d", &a, &b);
            add(a, b), add(b, a);
        }

        ans = 0;
        int cnt = 0;  // 记录连通块的数目
        for (root = 0; root < n; root++)  // 节点编号从0~n-1
            if (!dfn[root]) {
                cnt++;
                tarjan(root);
            }

        printf("%d\n", cnt + ans - 1);
    }

    return 0;
}