无向图的双连通分量原理

• 双联通分量也被称为重连通分量，一下内容都是针对无向图来说的。

• 无向图的双联通分量可以分为两类：

（1）边双联通分量（e-DCC）；

（2）点双联通分量（v-DCC）；

• 对于（1）边双联通分量的定义，我们需要引入桥的概念，桥是指连通图中的一条边，这条边满足：如果删除这条边，整个图会变的不连通，则这条边被称为桥。极大的不含有桥的连通区域称为边连通分量。根据定义可知e-DCC有以下性质：

① 在e-DCC中，无论删除哪条边，该e-DCC仍是连通的；

② 在e-DCC中，任意两点之间至少存在两条不相交（边是严格不相交的，点可以相交）的路径；

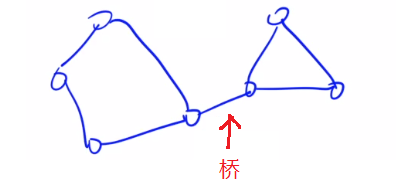
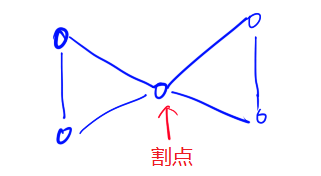
• 对于（2）点双联通分量的定义，我们需要引入割点的概念，割点是指连通图中的一个点，这个点满足：如果删除这个点以及该点相关联的所有边，整个图会变的不连通，则这个点被称为割点。极大的不含有割点的连通区域称为点连通分量。根据定义可知v-DCC有以下性质：

① 每个割点至少属于两个v-DCC

• 割点和桥之间没有任何关系

（1）两个割点之间的边一定是桥吗？不一定是，如下图：

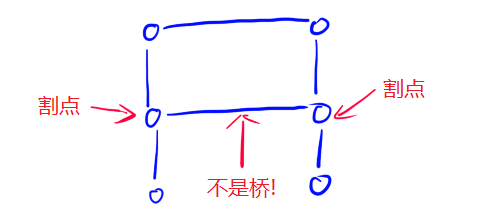
（2）一个桥的两个端点一定是割点吗？不一定是，如下图：

• 边连通分量和点连通分量之间也没有任何关系

（1）一个图是边连通分量，则它一定是点连通分量吗？不一定是，如下图：

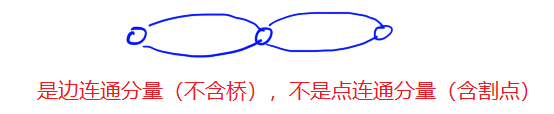
（2）一个图是点连通分量，则它一定是边连通分量吗？不一定是，如下图：

• 对于一棵树来说，所有的边都是桥，因此树中的每个点都是一个边连通分量；除叶节点外的所有节点都是割点，因此每条边以及边的两个端点构成的图都是点连通分量。

• 如何求解边双联通分量？这里的做法和求有向图的强联通分量（网址）是类似的，也需要时间戳以及$dfn、low$数组。

• 引入时间戳（从1开始计数）的概念，根据DFS过程中每个节点遍历到的顺序依次给每个节点递增赋值。

• 对于每个节点，定义两个时间戳：$dfn[u]$和$low[u]$。

$dfn[u]$：表示遍历到u的时间戳；

low[u]：从u开始走，所能遍历到的最小时间戳。

• 如何找到所有的桥？边(x, y)是桥$\iff dfn[x] < low[y]$。

• 如何找到所有的边连通分量？存在两种做法：

（1）将所有的桥删除，剩余的每个连通分量就是e-DCC。

（2）类似于有向图求SCC，可以使用一个栈记录当前边连通分量中的点，如果有$dfn[u] == low[u]$，说明此时递归过程中走到x的边是桥，此时可以弹出栈中的元素，得到一个e-DCC。

分析

• 在一个连通图中，任意两点之间至少存在两条不相交（边是严格不相交的，点可以相交）的路径$\iff$这个图是一个边双联通分量。这里不给证明，记住结论即可。

• 根据上面的结论，则这个题目相当于问：给我们一个无向连通图，问至少加几条边，可以将其变为一个边双联通分量（e-DCC）。注意可以认为AcWing 367. 学校网络是这一题的有向图版本，问的是有向图中加几条边能够成为SCC。

• 具体的做法是：将图中所有的边连通分量进行缩点，缩点完成后的新图就会变成一棵树，对于树中所有的叶子节点（假设有cnt个），我们都至少要给他们加上一条边，因此我们至少需要给图中添加$\lceil cnt/2 \rceil = \lfloor (cnt+1)/2 \rfloor$条边。

• 因此，最终的结论是：

（1）在一个无向连通图中，如果该图原本就是一个e-DCC，则不需要加边就满足条件；对图中所有e-DCC缩点之后图会变成一棵树，若新图中叶节点个数为cnt，则图中添加$\lceil cnt/2 \rceil = \lfloor (cnt+1)/2 \rfloor$条边即可让整张图变为一个e-DCC。对应本题。

（2）在一个有向图中，如果该图原本就是一个SCC，则不需要加边就满足条件；否则对图中所有的SCC进行缩点之后，若起点有P个，终点有Q个，则至少增加$MAX(P, Q)$条边即可让整个有向图成为一个SCC。对应AcWing 367. 学校网络。

#include <iostream>
#include <cstring>

using namespace std;

const int N = 5010, M = 20010;

int n, m;
int h[N], e[M], ne[M], idx;

int dfn[N];  // dfn[u]: 表示遍历到u的时间戳
int low[N];  // low[n]: 从u开始走，所能遍历到的最小时间戳。
int timestamp;  // 时间戳

int stk[N], top;  // 存储在当前e-DCC中的点

int id[N];  // 表示某个点所在的e-DCC编号
int dcc_cnt;  // 表示当前有多少个e-DCC

bool is_bridge[M];  // 记录每条边是否是桥

int d[N];  // 每个e-DCC的度数

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

// 点u是从边from过来的，防止从u向边from回搜
void tarjan(int u, int from) {

    dfn[u] = low[u] = ++ timestamp;
    stk[++top] = u;

    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (!dfn[j]) {
            tarjan(j, i);
            low[u] = min(low[u], low[j]);
            if (dfn[u] < low[j])  // 说明从j无法回到前面，(u, j)是桥
                is_bridge[i] = is_bridge[i ^ 1] = true;
        } else if (i != (from ^ 1))  // 第i条边不能是回去的边
            low[u] = min(low[u], dfn[j]);
    }

    if (dfn[u] == low[u]) {
        ++dcc_cnt;
        int y;
        do {
            y = stk[top--];
            id[y] = dcc_cnt;
        } while (y != u);
    }
}

int main() {

    cin >> n >> m;
    memset(h, -1, sizeof h);
    while (m--) {
        int a, b;
        cin >> a >> b;
        // 第0条边和第1条边是一对，之后类似
        // 如果知道其中一条边的是第i条边，则另一条边是第i^1条边
        add(a, b), add(b, a);
    }

    tarjan(1, -1);

    // idx记录的边的数目
    // 统计每个e-DCC的出度
    for (int i = 0; i < idx; i++)
        if (is_bridge[i])
            d[id[e[i]]]++;

    // 统计叶子节点的数目
    int cnt = 0;
    for (int i = 1; i <= dcc_cnt; i++)
        if (d[i] == 1)
            cnt++;

    printf("%d\n", (cnt + 1) / 2);

    return 0;
}