Blog
思路

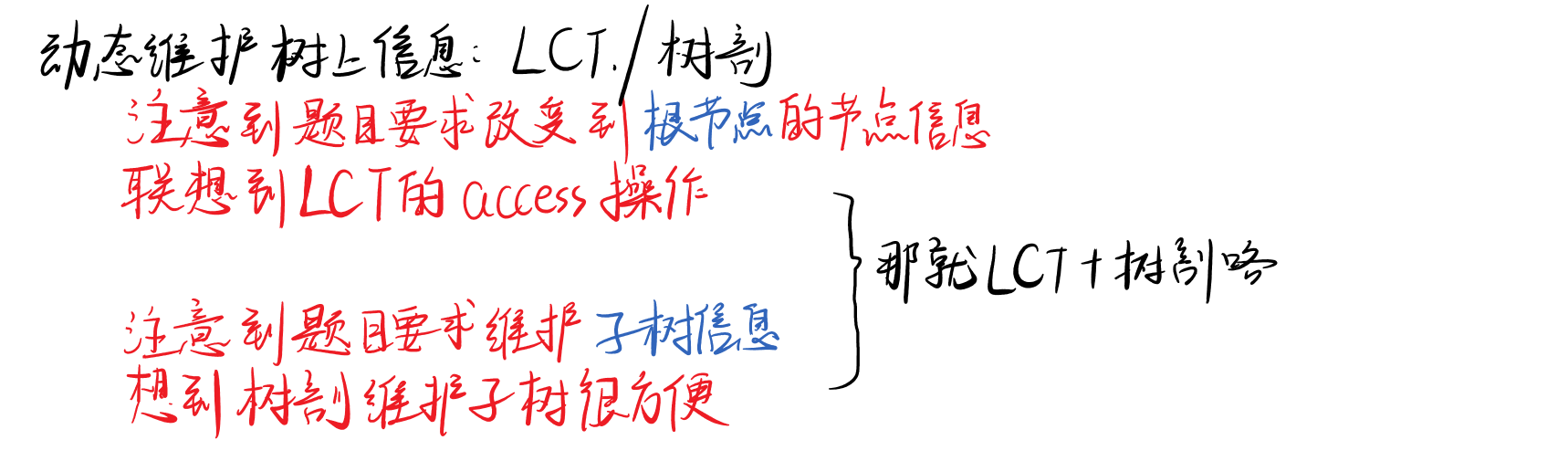
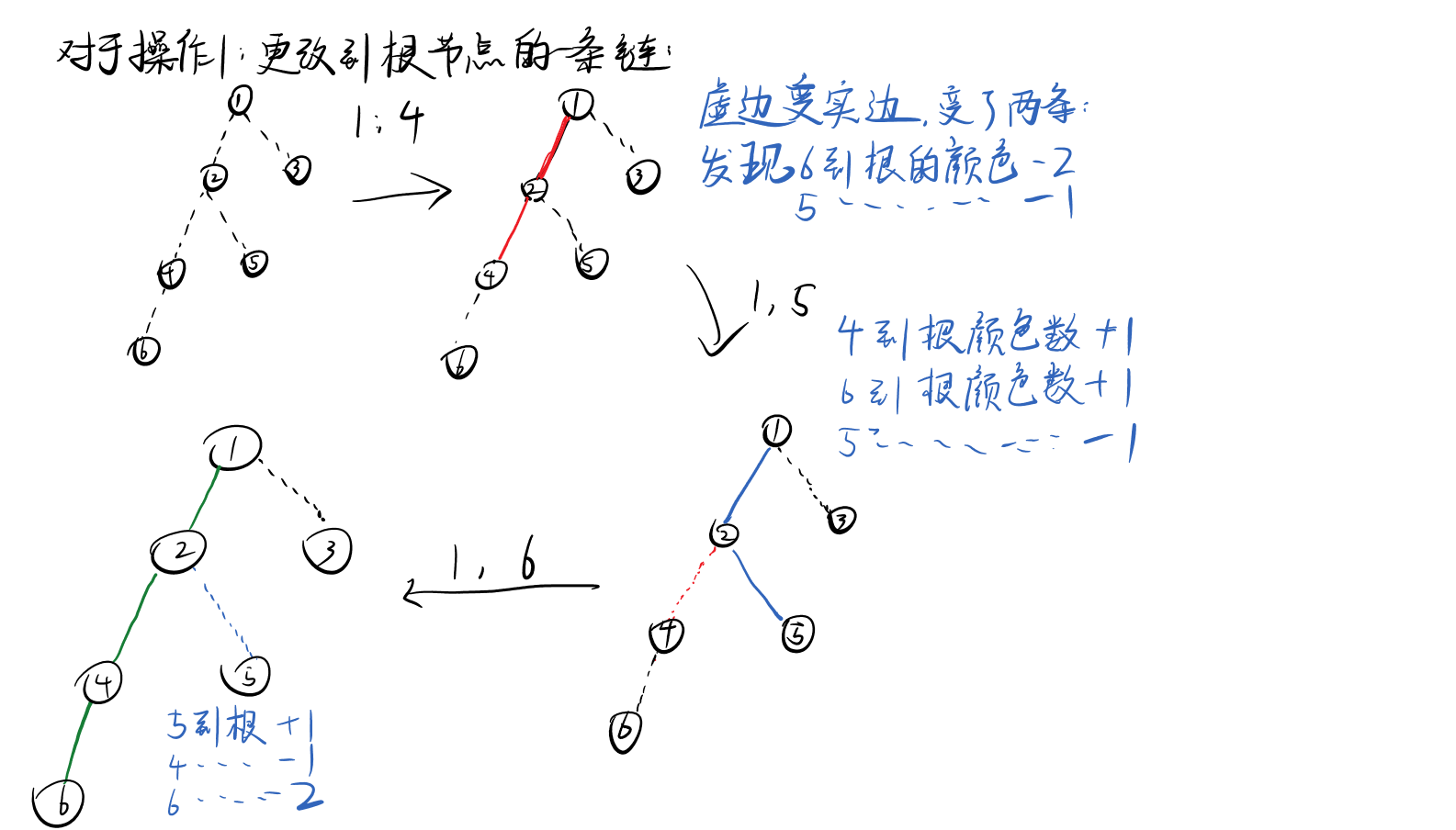


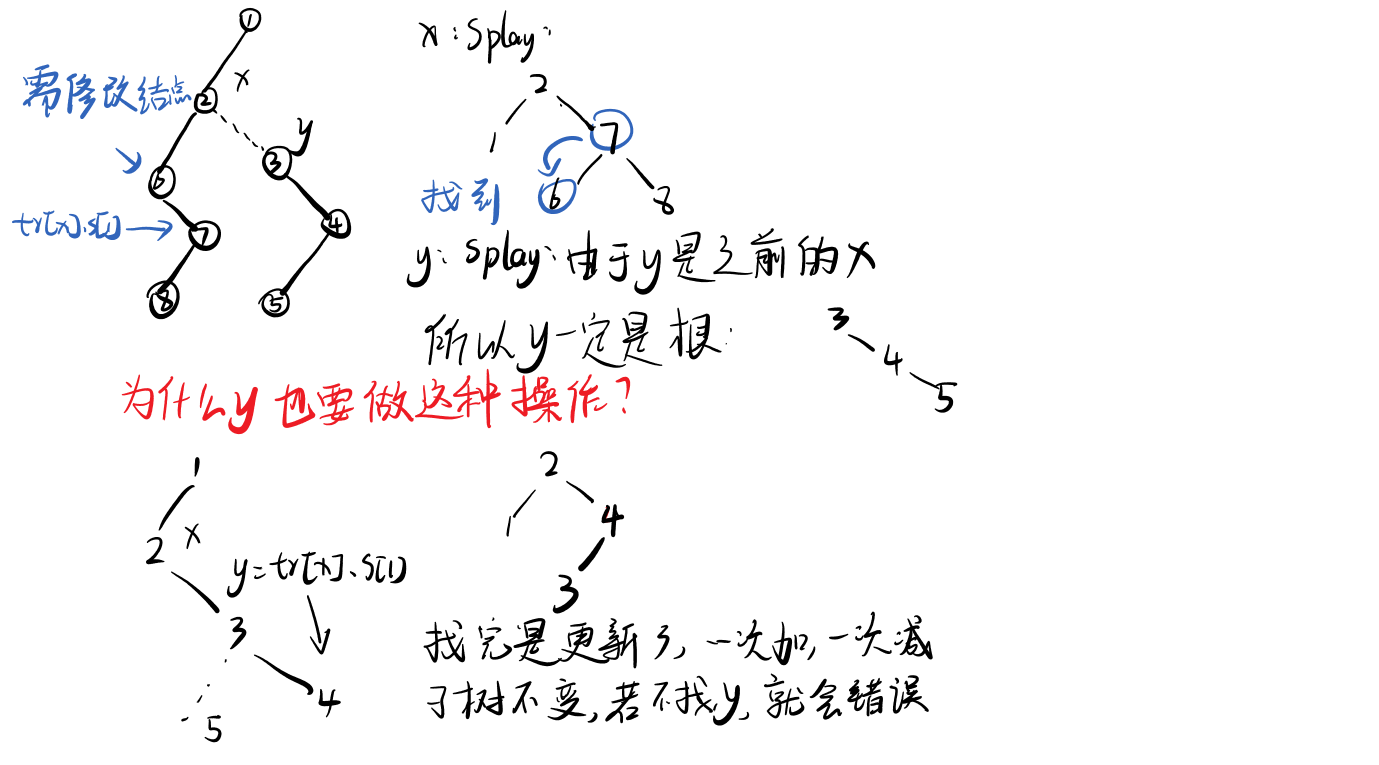



代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100010;
int n, m;
int h[N], ptr[N], val[N], idx;
struct NODE { int s[2], p; } tr[N];
void add(int a, int b) { val[idx] = b, ptr[idx] = h[a], h[a] = idx++; }
/***** Begin 树剖 *****/
// 重链顶点, 父亲节点, 深度, 重儿子, 子树大小
int top[N], fa[N], dep[N], son[N], sz[N]{1};
// id[u] -> u 这个点对应的dfn序中的下标, nw -> 新的序列
int id[N], nw[N], cnt;
void DFS_init(int u, int f, int d) {
dep[u] = d, tr[u].p = fa[u] = f, sz[u] = 1;
for (int i = h[u], v = val[i]; i != -1; i = ptr[i], v = val[i]) {
if (v == f) continue;
DFS_init(v, u, d + 1), sz[u] += sz[v];
if (sz[son[u]] < sz[v]) son[u] = v;
}
}
void DFS_seq(int u, int t) {
// dfn序列初始值设为深度, 对答案没有影响, 因为同级之间没有影响
top[u] = t, id[u] = ++cnt, nw[cnt] = dep[u];
if (son[u]) DFS_seq(son[u], t);
for (int i = h[u], v = val[i]; i != -1; i = ptr[i], v = val[i])
if (v != fa[u] && v != son[u]) DFS_seq(v, v);
}
// 顺便求个LCA
int LCA(int a, int b) {
while (top[a] != top[b]) {
if (dep[top[a]] < dep[top[b]]) swap(a, b);
a = fa[top[a]];
}
return (dep[a] > dep[b]) ? b : a;
}
/***** End 树剖 *****/
/***** Begin 线段树 *****/
// 左右区间, 最大值, add懒标记
int R[N << 2], L[N << 2], M[N << 2], A[N << 2];
void T_add(int u, int c) { M[u] += c, A[u] += c; }
void T_pushup(int u) { M[u] = max(M[u << 1], M[u << 1 | 1]); }
void T_pushdown(int u) { T_add(u << 1, A[u]), T_add(u << 1 | 1, A[u]), A[u] = 0; }
void build(int u, int l, int r) {
L[u] = l, R[u] = r;
if (l >= r) { M[u] = nw[l]; return; }
int mid = (l + r) >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
T_pushup(u);
}
void update(int u, int l, int r, int v) {
if (L[u] >= l && R[u] <= r) { A[u] += v, M[u] += v; return; }
T_pushdown(u);
int mid = (L[u] + R[u]) >> 1;
if (l <= mid) update(u << 1, l, r, v);
if (r > mid) update(u << 1 | 1, l, r, v);
T_pushup(u);
}
int query(int u, int l, int r) {
if (L[u] >= l && R[u] <= r) return M[u];
T_pushdown(u);
int mid = (L[u] + R[u]) >> 1, res = 0;
if (l <= mid) res = max(res, query(u << 1, l, r));
if (r > mid) res = max(res, query(u << 1 | 1, l, r));
return res;
}
/***** End 线段树 *****/
/***** Begin Splay *****/
bool isroot(int x) { return tr[tr[x].p].s[1] != x && tr[tr[x].p].s[0] != x; }
void rotate(int x) {
int y = tr[x].p, z = tr[y].p;
if (!isroot(y)) tr[z].s[tr[z].s[1] == y] = x;
tr[x].p = z;
int k = tr[y].s[1] == x;
tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
tr[x].s[k ^ 1] = y, tr[y].p = x;
}
void splay(int x) {
int y = tr[x].p, z = tr[y].p;
for (; !isroot(x); rotate(x), y = tr[x].p, z = tr[y].p)
if (!isroot(y)) rotate((tr[z].s[1] == y) ^ (tr[y].s[1] == x) ? x : y);
}
int find(int x) {
while (tr[x].s[0]) x = tr[x].s[0];
return x;
}
void access(int x) {
int t = x;
for (int y = 0; x; y = x, x = tr[x].p) {
splay(x);
int a = find(tr[x].s[1]), b = find(y);
if (a) update(1, id[a], id[a] + sz[a] - 1, 1);
if (b) update(1, id[b], id[b] + sz[b] - 1, -1);
tr[x].s[1] = y;
}
splay(t);
}
/***** End Splay *****/
int main() {
cin >> n >> m;
memset(h, -1, sizeof h);
for (int i = 1, a, b; i < n && cin >> a >> b; i++) add(a, b);
DFS_init(1, 0, 1), DFS_seq(1, 1), build(1, 1, n);
for (int op, a, b; m-- && cin >> op; ) {
if (op == 1) cin >> a, access(a);
else if (op == 2) {
cin >> a >> b;
int t = LCA(a, b), res = 0;
res += query(1, id[a], id[a]) + query(1, id[b], id[b]);
res -= query(1, id[t], id[t]) * 2;
cout << res + 1 << endl;
} else cin >> a, cout << query(1, id[a], id[a] + sz[a] - 1) << endl;
}
return 0;
}


赞!
完全懂了,非常感谢