分析

• 复杂度分析：如果我们一次拿出连续的i本书，则有n-i+1种选择。还剩下n-i本书，一共有n-i+1个位置可以插入这些书，除去原来的位置，则还有n-i个位置可以插入，将这些书放到某些书的后面，相当于将某些书放到这些书前面，因此最终的结果需要除以2，i可以从1取到15，因此选法有：
  $$ \frac{15\times14+14\times13+....+2\times1}{2} $$
  因为：
  $$ n\times(n-1)+(n-1)\times(n-2)+....+2\times1=\frac{(n-1)\times n\times(n+1)}{3} $$
  所以：
  $$ \frac{15\times14+14\times13+....+2\times1}{2}=\frac{14\times15\times16}{2\times3}=560 $$
  每层有560种选择，最多遍历4次，因此最多遍历：$560^4$=98,344,960,000

直接暴搜会超时。

• 我们可以采用双向宽搜，也可以采用IDA*，这里演示采用IDA*。

• 我们需要知道我们的估价函数值，这里我们考虑排好序后每个数的后继，n的后继应该是n+1，每次操作我们最多更改3个元素的后继关系，如下图：

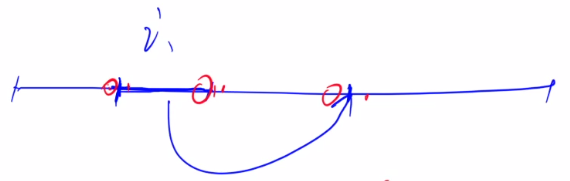
• 每次迭代前，我们可以计算出当前有多少个后继关系是不正确的，假设一共有tot个后继不正确，则修复这些后继需要的最少步数为：
  $$ \lceil \frac{tot}{3} \rceil = \lfloor \frac{tot+2}{3} \rfloor $$

• 如果当前的步数加上估价函数的值大于迭代加深的步数，则直接可以回溯。

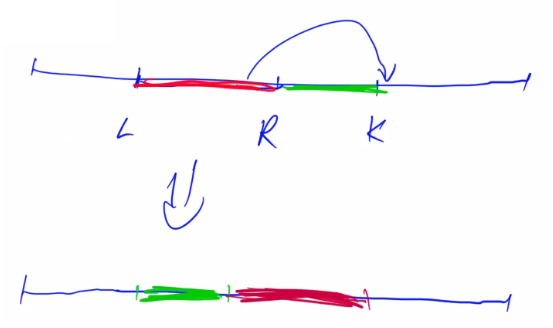
• 我们每次只需要枚举将长度为i的书放到后面的位置即可，如下图：

#include <iostream>
#include <cstring>

using namespace std;

const int N = 15;

int n;
int q[N];  // 书的编号
int w[5][N];  // 恢复现场使用

// 估价函数
int f() {
    int cnt = 0;
    for (int i = 0; i + 1 < n; i++)
        if (q[i + 1] != q[i] + 1)
            cnt++;
    return (cnt + 2) / 3;
}

// 检查序列是否已经有序
bool check() {
    for (int i = 0; i + 1 < n; i++)
        if (q[i + 1] != q[i] + 1)
            return false;
    return true;
}

// k: 当前迭代深度; depth: 迭代加深最大深度
bool dfs(int depth, int max_depth) {

    if (depth + f() > max_depth) return false;
    if (check()) return true;

    for (int len = 1; len <= n; len++)  // 先遍历长度
        for (int l = 0; l + len - 1 < n; l++) {  // 再遍历左端点
            int r = l + len - 1;
            for (int k = r + 1; k < n; k++) {
                memcpy(w[depth], q, sizeof q);
                int x, y;
                // 将上图中绿色部分移动到红色部分
                for (x = r + 1, y = l; x <= k; x++, y++) q[y] = w[depth][x];
                // 将上图中红色部分移动到绿色部分
                for (x = l; x <= r; x++, y++) q[y] = w[depth][x];
                if (dfs(depth + 1, max_depth)) return true;
                memcpy(q, w[depth], sizeof q);
            }
        }
    return false;
}

int main() {

    int T;
    cin >> T;

    while (T--) {
        cin >> n;
        for (int i = 0; i < n; i++) cin >> q[i];

        int depth = 0;
        while (depth < 5 && !dfs(0, depth)) depth++;
        if (depth >= 5) puts("5 or more");
        else cout << depth << endl;
    }

    return 0;
}