分析

• 根据题意，我们需要在图上去掉两条边，第一条是树边，第二条是非树边，然后使得图不连通，问这样的做法有多少种？

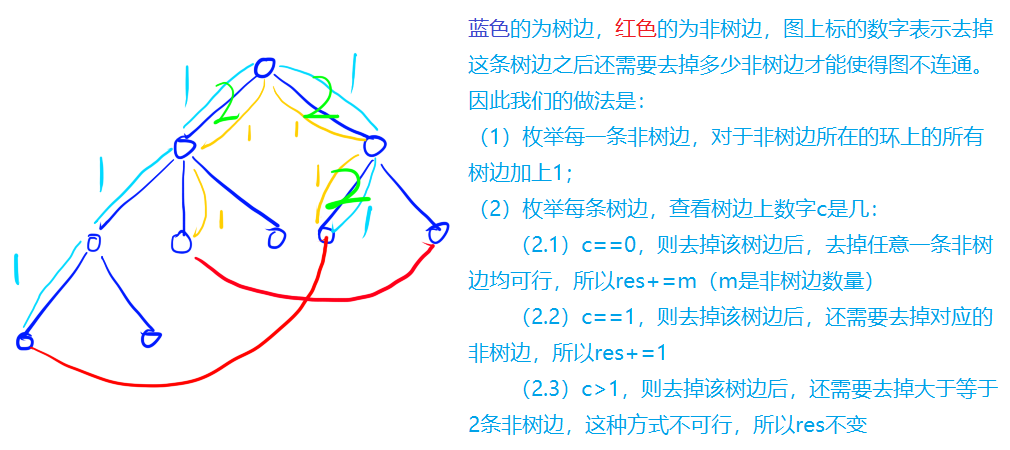
• 现在问题就变成了如何快速的给连续的树边上增加一个相同的值，并且快速的得到每个边上对应的值？这可以使用类似于差分的思想求解。做法如下：

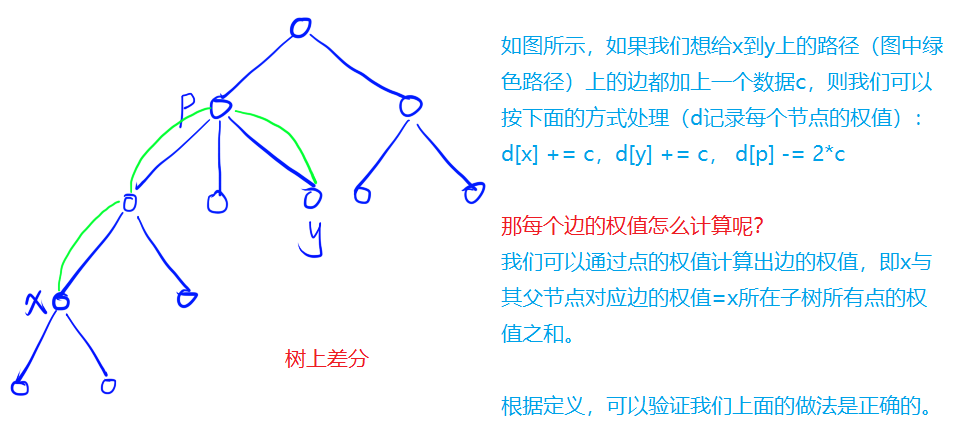
• 注意点：对于数组 $fa$ ，其第二维的大小应该为17，因为树中最多十万个点，$\lfloor log(100000) \rfloor = 16, (2^{16}=65536)$，因此 $fa$ 的第二维有0-16一共17个数，第二维需要设置为17。

#include <iostream>
#include <cstring>

using namespace std;

const int N = 100010, M = N * 2;  // 附加边不需要存储

int n, m;  // 点数、附加边数
int h[N], e[M], w[M], ne[M], idx;
int depth[N], fa[N][17];
int d[N];  // 树上差分，每个点上的权值，可以转化为边上的权值
int q[N];  // bfs使用到的队列
int ans;  // 方案数

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void bfs() {

    // 这里默认1号点为根节点，其实任意一个点都可以作为根节点
    memset(depth, 0x3f, sizeof depth);
    depth[0] = 0, depth[1] = 1;

    int hh = 0, tt = 0;
    q[0] = 1;

    while (hh <= tt) {

        int t = q[hh++];

        for (int i = h[t]; ~i; i = ne[i]) {
            int j = e[i];
            if (depth[j] > depth[t] + 1) {
                depth[j] = depth[t] + 1;
                q[++tt] = j;

                fa[j][0] = t;
                for (int k = 1; k <= 16; k++)
                    fa[j][k] = fa[fa[j][k - 1]][k - 1];
            }
        }
    }
}

int lca(int a, int b) {

    if (depth[a] < depth[b]) swap(a, b);

    for (int k = 16; k >= 0; k--)
        if (depth[fa[a][k]] >= depth[b])
            a = fa[a][k];

    if (a == b) return a;

    for (int k = 16; k >= 0; k--)
        if (fa[a][k] != fa[b][k]) {
            a = fa[a][k];
            b = fa[b][k];
        }

    return fa[a][0];
}

// fa: u的父节点，防止遍历出现环
// 返回以u为根的所有点的权值和
int dfs(int u, int fa) {

    int res = d[u];
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j != fa) {
            int s = dfs(j, u);
            if (s == 0) ans += m;
            else if (s == 1) ans += 1;
            res += s;
        }
    }
    return res;
}

int main() {

    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i++) {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a);
    }

    bfs();  // 求解depth、fa

    for (int i = 0; i < m; i++) {
        int a, b;
        scanf("%d%d", &a, &b);
        int p = lca(a, b);
        d[a]++, d[b]++, d[p] -= 2;
    }

    dfs(1, -1);

    printf("%d\n", ans);

    return 0;
}