分析

• 这一题和 AcWing 1148. 秘密的牛奶运输 一样，都是求解次小生成树，关于次小生成树的分析如下：

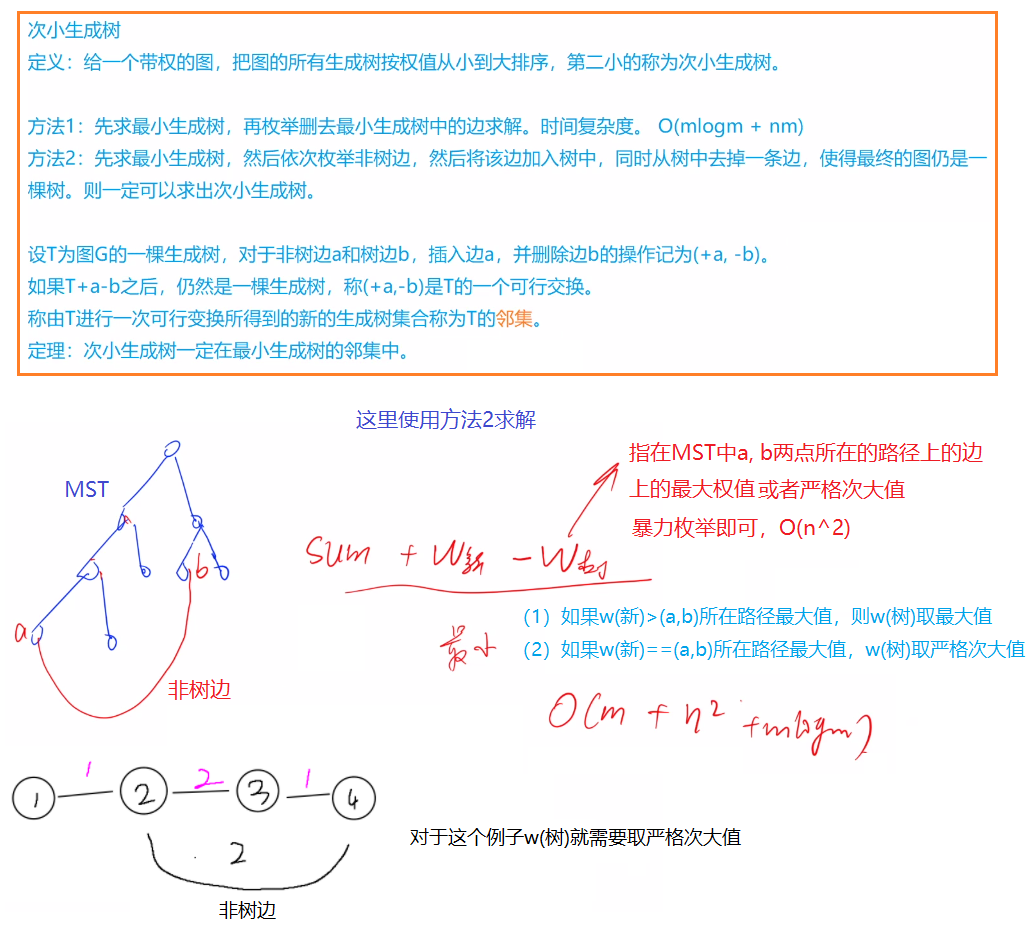
• 这一题对求解MST中任意两点之间的距离进行了优化处理，即上图中的暴力枚举，将$O(n^2)$的时间复杂度优化为$O(n \times log(n))$的时间复杂度，具体优化过程如下：

• 我们使用 $d1[i, j]$ 表示在节点i向上跳 $2^j$ 步路径上的边权最大值， $d2[i, j]$ 表示在节点i向上跳 $2^j$ 步路径上的边权严格次大值。在lca向上跳的过程中记录每次跳跃时的最大值和次大值，那么最终整个路径中的最大值和次大值一定在这些记录的值中，从中求出即可。

• 那么如何求解 $d1、d2$ 呢？和求 $fa$ 类似，在BFS的过程中递推求解即可，如下图：

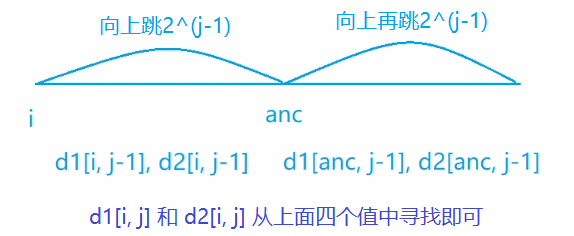
• 总结：求解这个题分为三步：

（1）使用kruskal算法求解最小生成树；

（2）求解 $d1、d2$ 数组；

（3）依次枚举每条非树边，将其加入树中，一定会形成环，去掉环中树边的最大值或者次大值得到另一棵树，这些树中权值最小的就是次小生成树。

• 注意点：对于数组 $fa、d1、d2$ ，其第二维的大小应该为17，因为树中最多十万个点，$\lfloor log(100000) \rfloor = 16, (2^{16}=65536)$，因此 $fa、d1、d2$ 的第二维有0-16一共17个数，第二维需要设置为17。另外邻接表中我们建立的是MST，双向边，最多二十万条边。边的存储使用结构体。

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 100010, M = 300010, INF = 0x3f3f3f3f;

int n, m;  // 点数、边数
int h[N], e[M], w[M], ne[M], idx;  // 存储MST
struct Edge {
    int a, b, w;
    int used;  // 该边是否在MST中
    bool operator< (const Edge &e) const {
        return w < e.w;
    }
} edges[M];
int p[N];  // kruskal算法使用到的并查集
int depth[N];  // 节点深度，根节点深度规定为1, depth[0]规定为0
int fa[N][17], d1[N][17], d2[N][17];
int q[N];  // bfs使用到的队列

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

LL kruskal() {

    for (int i = 1; i <= n; i++) p[i] = i;
    sort(edges, edges + m);
    LL res = 0;
    for (int i = 0; i< m; i++) {
        int a = find(edges[i].a), b = find(edges[i].b), w = edges[i].w;
        if (a != b) {
            p[a] = b;
            edges[i].used = true;
            res += w;
        }
    }

    return res;
}

void build() {

    memset(h, -1, sizeof h);
    for (int i = 0; i < m; i++) 
        if (edges[i].used) {
            int a = edges[i].a, b = edges[i].b, w = edges[i].w;
            add(a, b, w), add(b, a, w);
        }
}

void bfs() {

    // 这里默认1号点为根节点，其实任意一个点都可以作为根节点
    memset(depth, 0x3f, sizeof depth);
    depth[0] = 0, depth[1] = 0;
    int hh = 0, tt = 0;
    q[0] = 1;

    while (hh <= tt) {

        int t = q[hh++];

        for (int i = h[t]; ~i; i = ne[i]) {
            int j = e[i];
            if (depth[j] > depth[t] + 1) {
                depth[j] = depth[t] + 1;
                q[++tt] = j;

                fa[j][0] = t;
                d1[j][0] = w[i], d2[j][0] = -INF;
                for (int k = 1; k <= 16; k++) {
                    int anc = fa[j][k - 1];
                    fa[j][k] = fa[anc][k - 1];
                    int distance[4] = {d1[j][k - 1], d2[j][k - 1], d1[anc][k - 1], d2[anc][k - 1]};
                    d1[j][k] = d2[j][k] = -INF;
                    for (int u = 0; u < 4; u++) {
                        int d = distance[u];
                        if (d > d1[j][k]) d2[j][k] = d1[j][k], d1[j][k] = d;
                        else if (d != d1[j][k] && d > d2[j][k]) d2[j][k] = d;
                    }
                }
            }
        }
    }
}

LL lca(int a, int b, int w) {

    static int distance[N * 2];  // 记录上跳过程中每段的最大值和次大值
    int cnt = 0;  // 记录跳跃的次数，每跳一次，会记录两个数据

    if (depth[a] < depth[b]) swap(a, b);
    for (int k = 16; k >= 0; k--)
        if (depth[fa[a][k]] >= depth[b]) {
            distance[cnt++] = d1[a][k];
            distance[cnt++] = d2[a][k];
            a = fa[a][k];
        }

    if (a != b) {
        for (int k = 16; k >= 0; k--) 
            if (fa[a][k] != fa[b][k]) {
                distance[cnt++] = d1[a][k];
                distance[cnt++] = d2[a][k];
                distance[cnt++] = d1[b][k];
                distance[cnt++] = d2[b][k];
                a = fa[a][k], b = fa[b][k];
            }
        // 此时a,b到其LCA距离都为1，只存在最大值
        distance[cnt++] = d1[a][0];
        distance[cnt++] = d1[b][0];
    }

    int dist1 = -INF, dist2 = -INF;
    for (int i = 0; i < cnt; i++) {
        int d = distance[i];
        if (d > dist1) dist2 = dist1, dist1 = d;
        else if (d != dist1 && d > dist2) dist2 = d;
    }

    if (w > dist1) return w - dist1;
    return w - dist2;
}

int main() {

    scanf("%d%d", &n, &m);
    for (int i = 0; i < m; i++) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        edges[i] = {a, b, c};
    }

    LL sum = kruskal();  // 返回MST权值和
    build();  // 创建MST
    bfs();  // 求解fa、d1、d2

    LL res = 1e20;
    for (int i = 0; i < m; i++)
        if (!edges[i].used) {
            int a = edges[i].a, b = edges[i].b, w = edges[i].w;
            res = min(res, sum + lca(a, b, w));
        }

    printf("%lld\n", res);

    return 0;
}