分析

• 分析题目可知，此题让我们求解一个环，使得

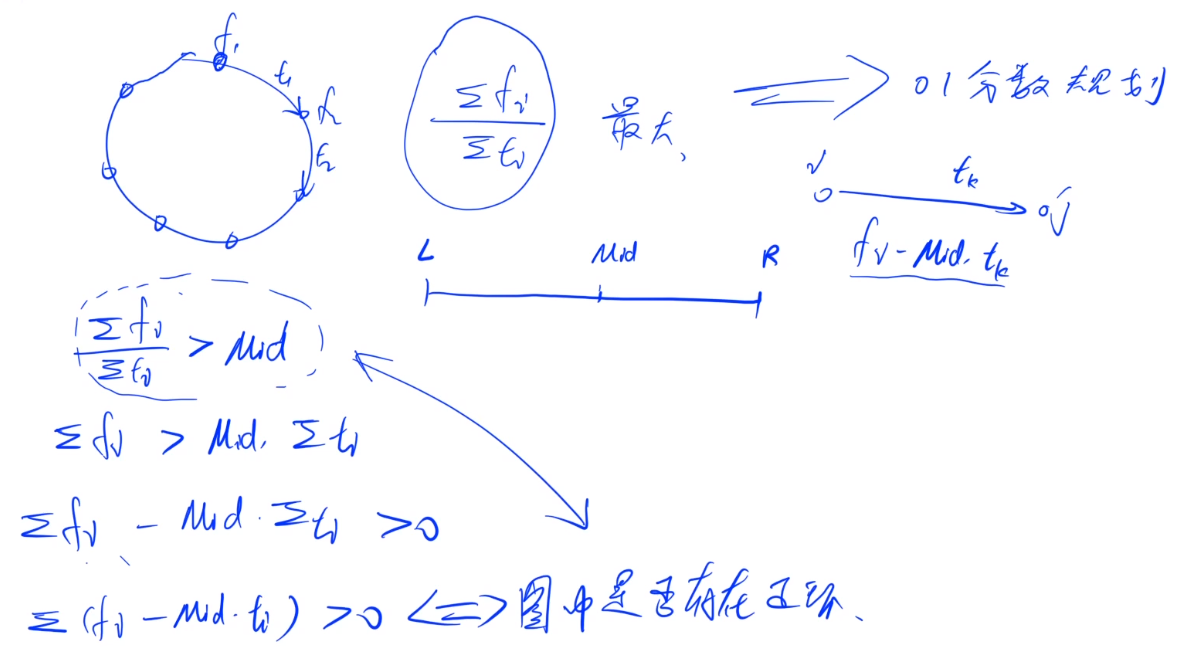
$$ \frac{\sum f_i}{\sum t_i} \quad f_i是环上的点的权值，t_i是环上边的权值 $$

取得最大值。

• 所有形如这样的问题，有一个统一的名称：01分数规划。这样的问题一般都可以采用二分来解决。

• 针对本题，因为$1\le f[i],t[i] \le 1000$，所以答案所在的范围是：(0, 1000]，可以对该区间进行二分。

• 对于区间[l, r]以及mid=(l + r) / 2，如果有

$$ \frac{\sum f_i}{\sum t_i} > mid $$

则说明答案在[mid, r]之间，否则答案在[l, mid]之间，接着二分即可。

• 对上面的不等式进行变形：

$$ \frac{\sum f_i}{\sum t_i} > mid \\ \sum f_i - mid \times \sum t_i > 0 \\ \sum (f_i-mid \times t_i) > 0 $$

• 根据上面的变形，我们可以将点上的权值变到出边上去，即每条边的权值变为$f_i-mid \times t_i$，这样方便我们处理。

• 在变换边权之后，最终问题就转化成了：图中是否存在正环。

• 那么如何求解正环呢？可以将所有的边权取个反，问题就变成了是否存在负环；但是实际上我们不需要这样做，我们只需要求最长路径即可。

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1010, M = 5010;

int n, m;
int wf[N];  // 每个点的权值
int h[N], e[M], wt[M], ne[M], idx;
double dist[N];
int cnt[N];  // cnt[i]表示到达i的最长路径经过的边数
int q[N];  // 循环队列
bool st[N];  // 代表点是否在队列中

void add(int a, int b, int c) {
    e[idx] = b, wt[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

bool check(double mid) {

    // 该函数会被调用多次，因此需要初始化cnt
    memset(cnt, 0, sizeof cnt);
    // dist不需要初始化，因为存在正环的话，到达该点的距离会被更新为+∞
    // st不需要初始化，因为最终队列为空，st的值会全部变为false

    int hh = 0, tt = 0;
    for (int i = 1; i <= n; i++) {
        q[tt++] = i;
        st[i] = true;
    }

    while (hh != tt) {

        int t = q[hh++];
        if (hh == N) hh = 0;

        st[t] = false;

        for (int i = h[t]; ~i; i = ne[i]) {
            int j = e[i];
            if (dist[j] < dist[t] + wf[t] - mid * wt[i]) {  // 求负环这里是>
                dist[j] = dist[t] + wf[t] - mid * wt[i];
                cnt[j] = cnt[t] + 1;
                if (cnt[j] >= n) return true;
                if (!st[j]) {
                    q[tt++] = j;
                    if (tt == N) tt = 0;
                    st[j] = true;
                }
            }
        }
    }

    return false;
}

int main() {

    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> wf[i];

    memset(h, -1, sizeof h);
    while (m--) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }

    double l = 0, r = 1010;
    while (r - l > 1e-4) {
        double mid = (l + r) / 2;
        if (check(mid)) l = mid;
        else r = mid;
    }

    printf("%.2lf\n", l);

    return 0;
}