分析

• 半连通子图只需要满足图中的点单向可到达即可（当然双向可到达也是可以的），根据定义可知强联通分量一定是半连通子图。

• 另外如果固定了点，则导出子图一定也是固定的，与之相关的边必须全部选上，即使是重边也必须全部选上。

• 因此我们的做法是：①首先求解强联通分量，②然后缩点，建图（注意重边需要判重）③最后在DAG上找到一个最长链（所谓最长是指链上的点最多），这条链上的点的数目就是最大半连通子图的点的数目

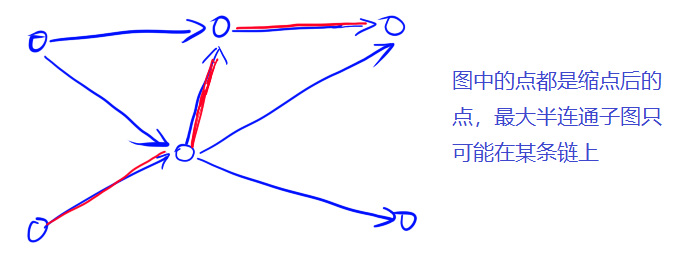
• 因为是拓扑图，所以可以采用递推的方式求解最大半连通子图中点的数目以及对应的方案数，本质上是一个DP。
• 定义$f[i]$和$g[i]$。

（1）$f[i]$：表示以第 i 个点为终点的最长链节点数量之和；

（2）$g[i]$：让$f[i]$取到最大值对应的方案数；

• 如果存在一条从i到k的边，则状态转移如下：

（1）如果$f[k] < f[i]+scc\_size[k]$，则$f[k]=f[i]+scc\_size[k], g[k]=g[i]$；

（2）如果$f[k] == f[i]+scc\_size[k]$，则$g[k]+=g[i]$；

• 另外对于重边我们只需要判断一次即可，需要去重，使用哈希表即可，如果边是$(a, b)$，则哈希函数设为$a \times 1000000ll + b$。

#include <iostream>
#include <cstring>
#include <unordered_set>

using namespace std;

typedef long long LL;

const int N = 100010, M = 2000010;  // 因为要建新图，两倍的边

int n, m, mod;  // 点数、边数、取模的数
int h[N], hs[N], e[M], ne[M], idx;  // h: 原图；hs: 新图
int dfn[N], low[N], timestamp;
int stk[N], top;
bool in_stk[N];
int id[N], scc_cnt, scc_size[N];
int f[N], g[N];

void add(int h[], int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void tarjan(int u) {

    dfn[u] = low[u] = ++timestamp;
    stk[++top] = u, in_stk[u] = true;

    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (!dfn[j]) {
            tarjan(j);
            low[u] = min(low[u], low[j]);
        } else if (in_stk[j])
            low[u] = min(low[u], dfn[j]);
    }

    if (dfn[u] == low[u]) {
        ++scc_cnt;
        int y;
        do {
            y = stk[top--];
            in_stk[y] = false;
            id[y] = scc_cnt;
            scc_size[scc_cnt]++;
        } while (y != u);
    }
}

int main() {

    memset(h, -1, sizeof h);
    memset(hs, -1, sizeof hs);

    scanf("%d%d%d", &n, &m, &mod);
    while (m--) {
        int a, b;
        scanf("%d%d", &a, &b);
        add(h, a, b);
    }

    // (1) 求SCC
    for (int i = 1; i <= n; i++)
        if (!dfn[i])
            tarjan(i);

    // (2) 缩点，建图
    unordered_set<LL> S;  // 判断是否为重边 (u, v) -> u * 1000000ll + v
    for (int i = 1; i <= n; i++)
        for (int j = h[i]; ~j; j = ne[j]) {
            int k = e[j];
            int a = id[i], b = id[k];
            LL hash = a * 1000000ll + b;
            if (a != b && !S.count(hash)) {
                add(hs, a, b);
                S.insert(hash);
            }
        }

    // (3) 根据拓扑序遍历DAG，从scc_cnt向前遍历自然满足拓扑序
    // 求解数组f和g
    for (int i = scc_cnt; i; i--) {
        if (!f[i]) {  // 说明是入度为0的点
            f[i] = scc_size[i];
            g[i] = 1;
        }
        for (int j = hs[i]; ~j; j = ne[j]) {
            int k = e[j];  // 边(i, k)
            if (f[k] < f[i] + scc_size[k]) {
                f[k] = f[i] + scc_size[k];
                g[k] = g[i];
            } else if (f[k] == f[i] + scc_size[k])
                g[k] = (g[k] + g[i]) % mod;
        }
    }

    // (3) 求解答案
    int maxf = 0, sum = 0;  // 最大半连通子图节点数、对应方案数
    for (int i = 1; i <= scc_cnt; i++)
        if (f[i] > maxf) {
            maxf = f[i];
            sum = g[i];
        }
        else if (f[i] == maxf) sum = (sum + g[i]) % mod;

    printf("%d\n", maxf);
    printf("%d\n", sum);

    return 0;
}