分析

• 本题相当于给了我们一张有向图，一旦一个点得到一个软件，这个点就可以将这个软件传给它指向的边，以此类推，然后问我们两个问题：

（1）我们至少需要将一个软件给多少个点，然后所有的点都可以得到这个软件？

（2）如果我们将一个软件给任意一个点，则其他点都能得到这个软件，需要至少条件多少边？（至少加几条边，可以将整个图变为一个SCC）

• 我们可以考虑缩点之后的新图，假设新图中有P个起点（即入度为0的点），Q个终点（即出度为0的点）。则第（1）问的答案是P，这是因为我们至少发P个，发P个之后每个点都能得到这个软件；第（2）问的答案是MAX(P, Q)，另外如果原图本来就是一个SCC，则答案是0，需要特判一下。

• 关于第（2）问答案的证明，因为起点和终点是对称的，不妨设$|P| \le |Q|$，证明一下答案是$|Q|$。

① 如果$|P|==1$，我们只需要让所有终点向起点连一条边，即新增$|Q|$条边，即可让整个图变为一个SCC；

② 如果$|P|>1$，则$|Q| \ge |P| > 1$，则至少存在两个起点，而且这两个起点到达两个不同的终点（可以用反证法证明这一点，假设如果找不到这样的两个起点，则所有的起点必定都到达一个终点，和$|Q| \ge2$矛盾），我们可以像下图那样添加边：

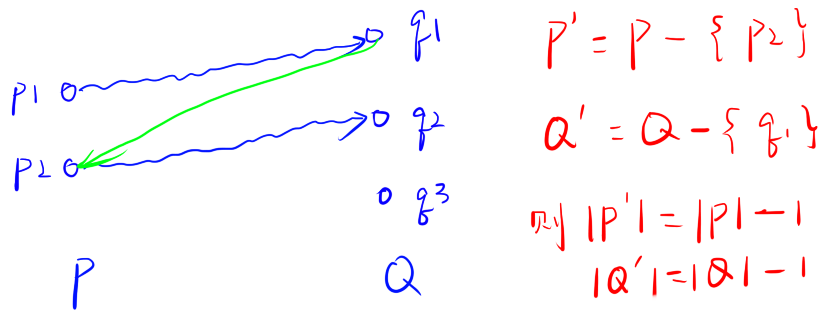
只要我们添加一条边，起点终点数量都为减少一个。因为当我们添加$|P|-1$条边后，只有一个起点了，此时还有$|Q|-(|P|-1)$个终点，根据①，此时还需要增加$|Q|-(|P|-1)$即可让整个图变为一个SCC；因此需要增加的边数为：$|P|-1+|Q|-(|P|-1)=|Q|$条边。证明完毕。

#include <iostream>
#include <cstring>

using namespace std;

const int N = 110, M = 10010;

int n;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], timestamp;
int stk[N], top;
bool in_stk[N];
int id[N], scc_cnt;
int din[N], dout[N];  // 每个SCC的入度、出度

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void tarjan(int u) {

    dfn[u] = low[u] = ++ timestamp;
    stk[++top] = u, in_stk[u] = true;

    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (!dfn[j]) {
            tarjan(j);
            low[u] = min(low[u], low[j]);
        } else if (in_stk[j]) low[u] = min(low[u], dfn[j]);
    }

    if (dfn[u] == low[u]) {
        ++ scc_cnt;
        int y;
        do {
            y = stk[top--];
            in_stk[y] = false;
            id[y] = scc_cnt;
        } while (y != u);
    }
}

int main() {

    cin >> n;
    memset(h, -1, sizeof h);
    for (int i = 1; i <= n; i++) {
        int t;
        while (cin >> t, t) add(i, t);
    }

    for (int i = 1; i <= n; i++)
        if (!dfn[i])
            tarjan(i);

    for (int i = 1; i <= n; i++)
        for (int j = h[i]; ~j; j = ne[j]) {
            int k = e[j];  // (i, k)
            int a = id[i], b = id[k];
            if (a != b) {
                dout[a]++;
                din[b]++;
            }
        }

    int P = 0, Q = 0;
    for (int i = 1; i <= scc_cnt; i++) {
        if (!din[i]) P++;
        if (!dout[i]) Q++;
    }

    printf("%d\n", P);
    if (scc_cnt == 1) puts("0");
    else printf("%d\n", max(P, Q));

    return 0;
}