原理

• 强连通分量是针对有向图来说的。如下的讲解默认都是针对有向图的。

• 连通分量：对于一个有向图中的一些点来说，如果任意两点都能相互到达，则称这些点以及对应的边构成连通分量。

• 强连通分量：指极大连通分量。即该联通分量中增加任何一个点都不能构成连通分量了。

• 那么强连通分量有什么作用呢？

我们可以通过使用求解强联通分量的方式将一个有向图缩点成有向无环图（DAG），也称为拓扑图。缩点：指将强联通分量缩成一个点。

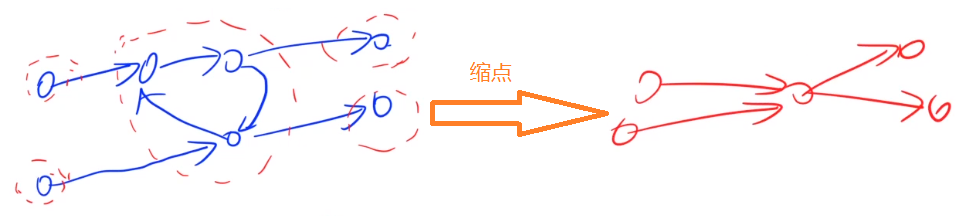
转化为拓扑图有什么好处呢？其中一个好处是我们在求解最短路/最长路的时候可以使用递推的方式求解。

• 下面就要考虑如何求解强联通分量了，我们采用DFS的方式求解。下面首先介绍一下在DFS过程中的各种边的分类：

（1）树枝边（x, y）：x是y的父节点；

（2）前向边（x, y）：x是y的祖先节点，因此树枝边是一种特殊的前向边；

（3）后向边（x, y）：y是x的祖先节点，并且从x还能回到y，这样回去的边（x, y）称为后向边；

（4）横叉边（x, y）：从当前DFS路径上的点x连向已经搜索完毕的的点y的边。

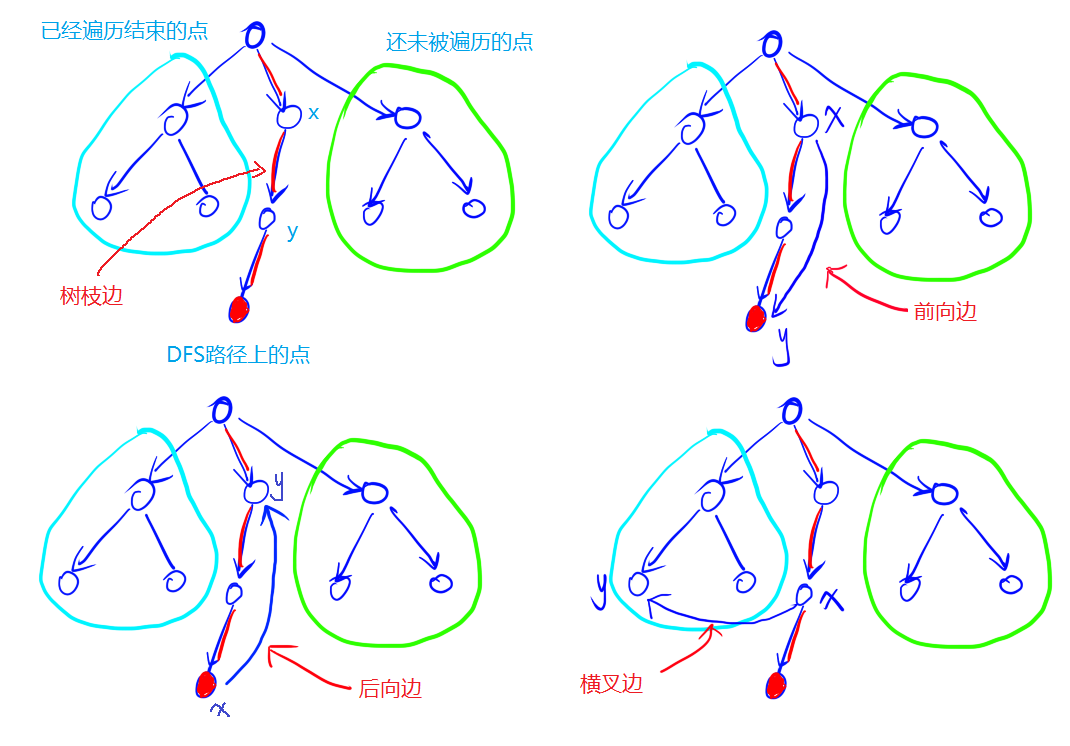
• 我们只需要熟悉一下这几个名词即可。

• 如何判断某个点x是否在一个强联通分量中呢？存在以下两种情况：

（1）存在后向边指向祖先节点；

（2）从当前点x可以经过横插边边走到点y，点y可以走到x的祖先节点。

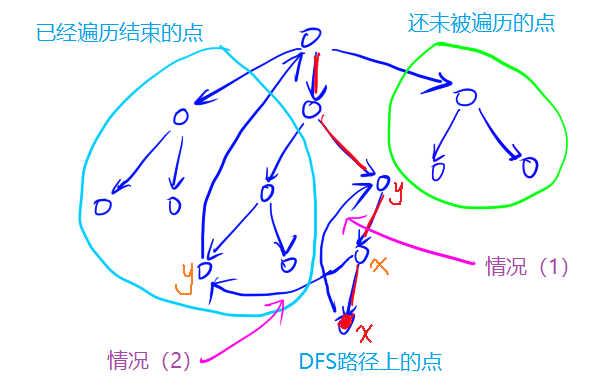
• 基于上面的原理，我们直接给出求SCC的算法，即tarjan算法。

• 这里引入时间戳（从1开始计数）的概念，根据DFS过程中每个节点遍历到的顺序依次给每个节点递增赋值。对于树枝边和前向边（x, y），y的时间戳大于x的时间戳；对于后向边和横叉边（x, y），y的时间戳小于x的时间戳。

• 对于每个节点，定义两个时间戳：$dfn[u]$和$low[u]$。

$dfn[u]$：表示遍历到u的时间戳；

low[u]：从u开始走，所能遍历到的最小时间戳。

• 我们每次求解的是每个强连通分量所在的最高点。如果u是其所在的强联通分量的最高点$\iff dfn[u]==low[u]$。

• 该做法的证明这里略过，这个证明一般使用不到。

• 因为每个点我们只会遍历一次，时间复杂度一般是$O(n+m)$的。

• 求完强联通分量之后就可以缩点了，设$id[u]$表示点u所在的强连通分量的编号（求SCC的时候可以求出来），则缩点过程如下：

for (int i = 1; i <= n; i++)
    for (i的所有临点j)
        if (id[i] != id[j])
            加一条id[i]到id[j]的新边

• 做完tarjan算法之后，强联通分量按照编号递减的顺序就已经是拓扑序了，因此后面就不需要再做一遍拓扑排序了（这是因为求拓扑序存在两种做法，一种是我们最熟悉的宽搜；另一种是深搜，将深搜过程中遍历到的点记录到seq中，则seq的逆序就是拓扑序）

分析

• 如果A认为B受欢迎，则从A向B连接一条有向边。

• 这一题可以使用floyd算法求闭包，然后统计每个点的入度是不是n-1，如果是的话说明该头牛被所有其他的牛所欢迎。但是这种做法会超时。

• 考虑一下，如果这个图是DAG的话，如果存在大于等于两个点的出度为0，则说明没有一头牛符合要求；如果只有一个点的出度为0，则说明这头牛被所有其他的牛所欢迎。

• 因此我们可以考虑对这个图求强联通分量，然后缩点（即将每个SCC看成一个点）建图，然后看新图是不是只有一个点的出度为0，如果是的话，新图中该点对应原图中的SCC中点的数量就是答案。

• 其实我们没有必要真正将新图建立出来，我们只需要统计一下每个SCC的出度即可。

#include <iostream>
#include <cstring>

using namespace std;

const int N = 10010, M = 50010;

int n, m;  // 点数、边数
int h[N], e[M], ne[M], idx;

int dfn[N];  // dfn[u]: 表示遍历到u的时间戳
int low[N];  // low[n]: 从u开始走，所能遍历到的最小时间戳。
int timestamp;  // 时间戳

int stk[N], top;  // 存储在当前SCC中的点
bool in_stk[N];  // 表示某个点是否在栈中

int id[N];  // 表示某个点所在的SCC编号
int scc_cnt;  // 表示当前有多少个SCC
int sz[N];  // 表示每个SCC中点的数量

int dout[N];  // 表示每个SCC的出度是多少

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void tarjan(int u) {

    dfn[u] = low[u] = ++ timestamp;
    stk[++top] = u, in_stk[u] = true;  // 将当前点加入栈中

    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];
        if (!dfn[j]) {  // 如果点j没有被遍历过，则遍历j
            tarjan(j);
            low[u] = min(low[u], low[j]);
        } else if (in_stk[j])
            low[u] = min(low[u], dfn[j]);
    }

    if (dfn[u] == low[u]) {  // 说明u是当前SCC的最高点
        ++scc_cnt;
        int y;
        do {
            y = stk[top--];
            in_stk[y] = false;
            id[y] = scc_cnt;
            sz[scc_cnt]++;
        } while (y != u);
    }
}

int main() {

    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    while (m--) {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
    }

    // tarjan算法
    for (int i = 1; i <= n; i++)
        if (!dfn[i])
            tarjan(i);

    // 建图，这里只需要求出每个SCC的出度
    for (int i = 1; i <= n; i++)    
        for (int j = h[i]; ~j; j = ne[j]) {
            int k = e[j];  // 边(i, k)
            int a = id[i], b = id[k];  // i,k所在的SCC的编号
            if (a != b) dout[a]++;
        }

    int zeros = 0;  // 出队为0的SCC的数量
    int sum = 0;  // 出度为0的SCC中点的数量
    for (int i = 1; i <= scc_cnt; i++)
        if (!dout[i]) {
            zeros++;
            sum += sz[i];
            if (zeros > 1) {  // 多于一个SCC出队为0，没有满足条件的点
                sum = 0;
                break;
            }
        }

    printf("%d\n", sum);

    return 0;
}