yxc题解
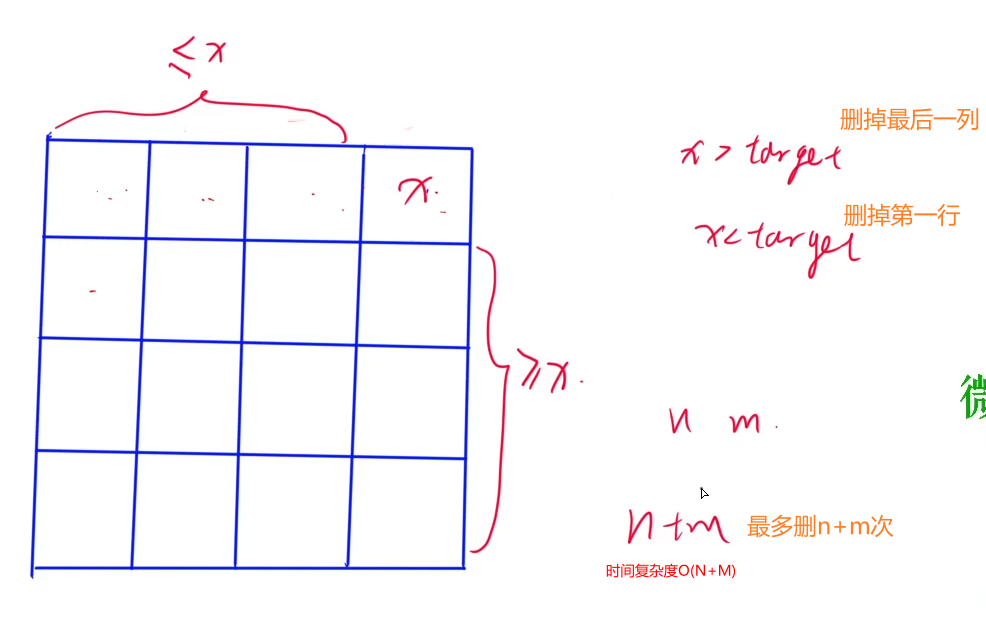
核心在于发现每个子矩阵右上角的数的性质：

• x左边的数都小于等于x，x下边的数都大于等于x。

因此我们可以从整个矩阵的右上角开始枚举，假设当前枚举的数是 x：

• 如果 x 等于target，则说明我们找到了目标值，返回true；
• 如果 x 小于target，则 x 左边的数一定都小于target，我们可以直接排除当前一整行的数；
• 如果 x 大于target，则 x 下边的数一定都大于target，我们可以直接排序当前一整列的数；

时间复杂度分析
每一步会排除一行或者一列，矩阵一共有 n 行，m 列，所以最多会进行 n+m 步。所以时间复杂度是 $O(n+m)$。

class Solution {
public:
    bool searchArray(vector<vector<int>> array, int target) {
        if (array.empty() || array[0].empty()) return false;
        int n = array.size(), m = array[0].size();
        int i = 0, j = m - 1;
        while (i < n && j >= 0) {
            int x = array[i][j];
            if (target == x) return true;
            else if (target > x) i ++; //排除一整行就是让枚举的点的横坐标加一，排除一整列就是让纵坐标减一
            else j --;
        }
        return false;//当我们排除完整个矩阵后仍没有找到目标值时，就说明目标值不存在，返回false。
    }
};

也可以选矩阵左下角点 为特殊点进行删行和列操作

class Solution {
public:
    bool searchArray(vector<vector<int>> array, int target) {
        if (array.empty() || array[0].empty()) return false;

        int n = array.size(), m = array[0].size();
        int i = n - 1, j = 0;
        while (i >= 0 && j <= m - 1) {
            if (target == array[i][j]) return true;
            else if (target > array[i][j]) j ++;
            else i --;
        }
        return false;
    }
};