图1：

图2：

如果此题去掉 题目的第二个条件：每行的第一个整数大于前一行的最后一个整数。怎么做？？（面试官会这样问！）

见 ACWing上的另一道题

AcWing 15. 二维数组中的查找

算法

(二分) $O(logn)$ 二分模板 （我之前写的题解）

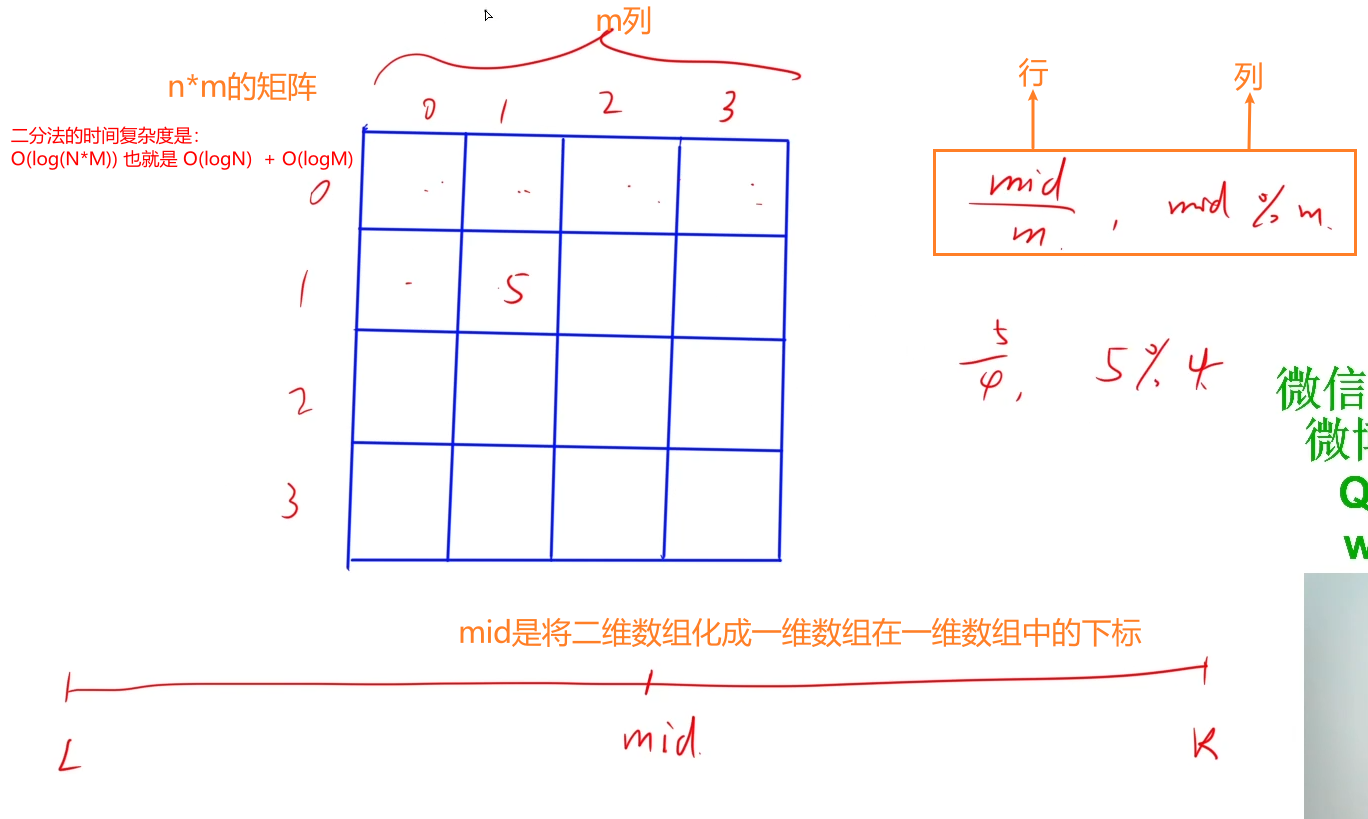
我们可以想象把整个矩阵，按行展开成一个一维数组，那么这个一维数组单调递增，然后直接二分即可。
二分时可以通过整除和取模运算得到二维数组的坐标。

时间复杂度分析：二分的时间复杂度是 $O(log(n*m))=O(logn) + O(logm)$

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        if (matrix.empty() || matrix[0].empty()) return false; //判断矩阵是否为空和矩阵的列是否为空
        int n =  matrix.size(), m = matrix[0].size();
        int l = 0, r = n * m - 1;
        while (l < r) {
            int mid = l + r >> 1;
            if (target <= matrix[mid / m][mid % m])  r = mid;
            else l = mid + 1;
        }
        return target == matrix[l/m][l%m];
    }
};

另一种二分写法：

        int n =  matrix.size(), m = matrix[0].size();
        int l = 0, r = n * m - 1;
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (target >= matrix[mid / m][mid % m])  l = mid;
            else r = mid - 1;
        }
        return target == matrix[r / m][r % m];