引用
看了大佬的题解深受启发
尘民 第十一届蓝桥杯 ——七段码
B1ackGod 蓝桥杯填空题总结(未完待续…
题目描述
小蓝要用七段码数码管来表示一种特殊的文字。
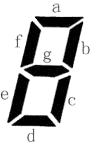
上图给出了七段码数码管的一个图示,数码管中一共有 7 段可以发光的二极管,分别标记为 a, b, c, d, e, f, g。
小蓝要选择一部分二极管(至少要有一个)发光来表达字符。在设计字符的表达时,要求所有发光的二极管是连成一片的。
例如:b 发光,其他二极管不发光可以用来表达一种字符。
例如:c 发光,其他二极管不发光可以用来表达一种字符。
这种方案与上一行的方案可以用来表示不同的字符,尽管看上去比较相似。
例如:a, b, c, d, e 发光,f, g 不发光可以用来表达一种字符。
例如:b, f 发光,其他二极管不发光则不能用来表达一种字符,因为发光的二极管没有连成一片。
请问,小蓝可以用七段码数码管表达多少种不同的字符?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。
本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
样例
无样例
算法
(并查集) $O(n)$
- 用 1 ~ 7 来代表 a ~ g;
- 若某两个二极管相邻,那么就在它们之间连一条边;
- 先用 dfs 枚举出二极管的所有亮灭情况;
- 再用 并查集 判断是否只有一个连通块;
首先我们用二维数组存相邻的两段,接着利用指数型枚举,求出所有的组合,然后利用并查集判断组合中的段是否连通并且只存在一个连通块即可
时间复杂度 $O(n)$
| 优化 | 平均时间复杂度 | 最坏时间复杂度 |
|---|---|---|
| 无优化 | $O(logn)$ | $O(n)$ |
| 路径压缩 | $O(\alpha(n))$ | $O(logn)$ |
| 按秩合并 | $O(logn)$ | $O(logn)$ |
| 路径压缩 + 按秩合并 | $O(\alpha(n))$ | $O(\alpha(n))$ |
C++ 代码
#include <iostream>
using namespace std;
const int N = 10;
int e[N][N] , p[N] , st[N];
int ans;
int find(int x)
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
void dfs(int u)
{
if(u > 7)
{
//初始化集合
for(int i = 1; i <= 7; i ++) p[i] = i;
//判断是否连通,并且这两段都被选了
for(int i = 1; i <= 7; i ++)
for(int j = 1; j <= 7; j ++)
if(e[i][j] && st[i] != 2 && st[j] != 2)
p[find(i)] = find(j);
int cnt = 0;
for(int i = 1; i <= 7; i ++)
if(st[i] != 2 && p[i] == i)
cnt ++;
//因为我们判断的时候是判断该组合中的段是否选了,并且父节点相同,
//而且题意又是只有连成一片才是算一种答案,所以只有在cnt为1的时候,才是我们要的组合,有可能是存在两个或以上的连通块
if(cnt == 1) ans ++;
return;
}
//0 待选
//1 选该段
//2 不选该段
st[u] = 1;
dfs(u + 1);
st[u] = 2;
dfs(u + 1);
}
int main()
{
//初始化相邻的段
e[1][2] = e[1][6] = 1;
e[2][1] = e[2][7] = e[2][3] = 1;
e[3][2] = e[3][7] = e[3][4] = 1;
e[4][3] = e[4][5] = 1;
e[5][4] = e[5][7] = e[5][6] = 1;
e[6][1] = e[6][7] = e[6][5] = 1;
e[7][2] = e[7][3] = e[7][5] = e[7][6] = 1;
dfs(1);
cout << ans << endl;
return 0;
}

