思考

多重背包问题与01背包不同的是，每件物品规定了至多选择的上限。

多重背包，完全背包可以在01背包的基础上多增加一重循环称为决策循环。即在总体积和物品数量的双重限制下的最大利润。

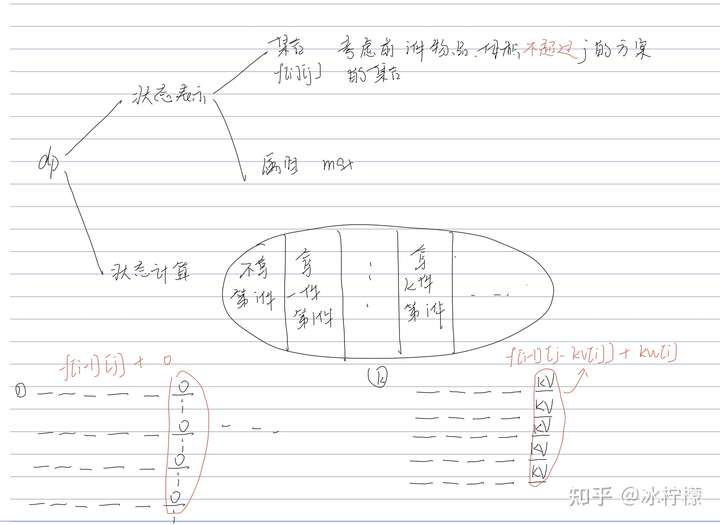
多重背包也可以理解为总共有s1+s2+s3+......+sn=t件物品的01背包问题
所以这题就有两种算法

算法一完全背包上两重限制代码

#include<iostream>
using namespace std;
const int N=110;
int n,m;
int v[N],w[N],s[N];
int f[N][N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i]>>s[i];
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i-1][j];
            for(int k=0;k*v[i]<=j&&k<=s[i];k++)
            {
                f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
            }
        }
    }
    cout<<f[n][m];
    return 0;
}

算法二拆分为01背包问题代码

我们可以看作总共有s1+s2+s3+......sn=t件物品，然后用01背包问题第一重for循环限制i<=t来解决就可以了

#include <bits/stdc++.h>
using namespace std;
int a[10005],b[10005],dp[10005];
int n,m;
int main()
{
    int t=0,w,v,s;
    cin>>n>>m;
    while(n--)
    {
        cin>>v>>w>>s;
        while(s--)
        {
            a[++t]=v;
            b[t]=w;
        }//死拆，把多重背包拆成01背包
    }
    for(int i=1;i<=t;i++)
    {
        for(int j=m;j>=a[i];j--)
        {
            dp[j] = max( dp[j-a[i]] + b[i] , dp[j] );//直接套01背包的板子
        }
    }
    cout<<dp[m]<<endl;
    return 0;
}