二分

首先对于为 $1$ 的点为起点，做一遍多源 $BFS$求出每个点距离运输处的最小值

现在考虑加入一个运输处使得每个点距离运输处的最小值的最大值最小，$BFS$ 得到的每个点距离运输处最小值的最大值记为 $maxx$，那么最终答案一定是介于 $1 \sim maxx$ 之间的，同时满足二段性

那么就可以二分答案，然后判断答案对应的值 $mid$ 是否满足即可：

现在问题转换成了从所有方格中挑出大于 $mid$ 的方格，然后放置一个运输处，使得这些点距离运输处的最小值都变成小于等于 $mid$，问是否存在这样的运输处

首先我们观察两个方格如果满足这样的条件：

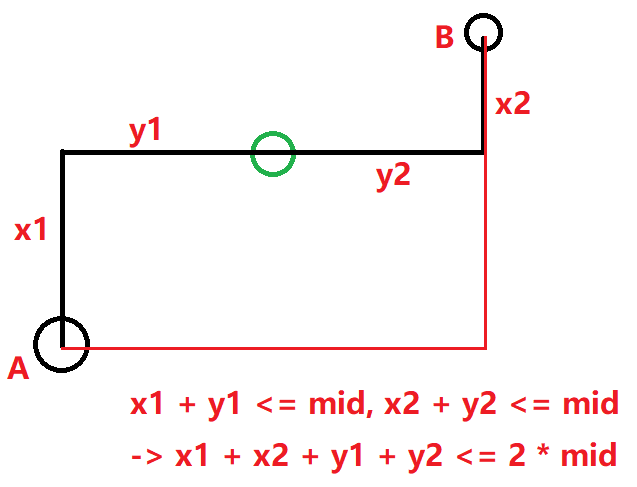
同时如果 $x_1 + x_2 + y_1 + y_2 \leq 2 * mid$, 那么就可以在 $A, B$ 这两个点构成的中间的矩形区域内任意找一个点作为运输处都是可以的，那么可知如果满足 $x_1 + x_2 + y_1 + y_2 \leq 2 * mid$，那么必然可以找到一个运输处，使得 $A, B$ 两个点都满足要求

那么可以得知：如果两个格子最后满足条件等价于两个点之间的曼哈顿距离小于等于 $2 * mid$

而对于两个点($A, B$)之间的曼哈顿距离可以等价于 $A$ 点距离 $(0, 0)$ 源点的曼哈顿距离 - $B$ 点距离 $(0, 0)$ 源点的曼哈顿距离（假设 $A$ 距离源点的曼哈顿距离大）, 而点 $(i, j)$ 距离 $(0, 0)$ 源点的曼哈顿距离为 $i + j$

因此：我们只需要遍历一遍所有挑出来的点，找到 $i + j$ 最大的 $maxx$ 和最小的 $minn$，然后判断：$maxx - minn \leq 2 * mid$ 即可

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
using PII = pair<int ,int >;
const int N = 256;

#define x first
#define y second

int n, m;
char g[N][N];
int d[N][N];
queue<PII > q;
bool st[N][N];

int bfs() {
    int dx[] = { -1, 0, 1, 0 };
    int dy[] = { 0, -1, 0, 1 };
    int res = 0;
    while (q.size()) {
        auto t = q.front(); q.pop();
        for (int i = 0; i < 4; ++i) {
            int a = t.x + dx[i], b = t.y + dy[i];
            if (a < 0 || a >= n || b < 0 || b >= m || st[a][b]) continue;
            d[a][b] = d[t.x][t.y] + 1;
            res = max(res, d[a][b]);
            st[a][b] = true;
            q.push({ a, b });
        }
    }
    return res;
}

bool check(int mid) {
    int minn = 1e8, maxx = 0;
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < m; ++j) {
            if (d[i][j] > mid) {
                minn = min(minn, i + j);
                maxx = max(maxx, i + j);
            }
        }
    }
    return maxx - minn <= 2 * mid;
}

int main() {
    int T;
    scanf("%d", &T);
    for (int cases = 1; cases <= T; ++cases) {
        scanf("%d%d", &n, &m);
        for (int i = 0; i < n; ++i) {
            scanf("%s", &g[i]);
            for (int j = 0; j < m; ++j) {
                st[i][j] = false;
                if (g[i][j] == '1') {
                    st[i][j] = true;
                    q.push({ i, j });
                }
                d[i][j] = 0;
            }
        }
        int maxx = bfs();
        int l = 0, r = maxx;
        while (l < r) {
            int mid = l + r >> 1;
            if (check(mid)) r = mid;
            else l = mid + 1;
        }
        printf("Case #%d: %d\n", cases, l);
    }

    return 0;
}