题目描述

$Z$国有$n$座城市，$n−1$条双向道路，每条双向道路连接两座城市，且任意两座城市都能通过若干条道路相互到达。  

$Z$国的国防部长小$Z$要在城市中驻扎军队。

驻扎军队需要满足如下几个条件： 

1. 一座城市可以驻扎一支军队，也可以不驻扎军队。 
2. 由道路直接连接的两座城市中至少要有一座城市驻扎军队。 
3. 在城市里驻扎军队会产生花费，在编号为$i$的城市中驻扎军队的花费是$p_i$。  
4. 小$Z$很快就规划出了一种驻扎军队的方案，使总花费最小。

但是国王又给小Z提出了$m$个要求，每个要求规定了其中两座城市是否驻扎军队。

小Z需要针对每个要求逐一给出回答。

具体而言，如果国王提出的第$j$个要求能够满足上述驻扎条件（不需要考虑第j个要求之外的其它要求），则需要给出在此要求前提下驻扎军队的最小开销。

如果国王提出的第$j$个要求无法满足，则需要输出$-1$ $(1 \le j \le m)$。

现在请你来帮助小$Z$。

输入格式

第1行包含两个正整数$𝑛,𝑚$和一个字符串 $\text{𝑡𝑦𝑝𝑒}$，分别表示城市数、要求数和数据类型。

$\text{𝑡𝑦𝑝𝑒}$是一个由大写字母$A，B$或$C$和一个数字$1，2，3$组成的字符串。

它可以帮助你获得部分分。

你可能不需要用到这个参数。

这个参数的含义在数据范围中有具体的描述。 

第$2$行$n$个整数$p_i$，表示编号i的城市中驻扎军队的花费。 

接下来$n−1$行，每行两个正整数$u,v$，表示有一条u到v的双向道路。 

接下来m行，第j行四个整数$a,x,b,y$ $(a≠b)$，表示第j个要求是在城市$a$驻扎$x$支军队，在城市$b$驻扎$y$支军队。

其中，$x$ 、 $y$ 的取值只有$0$或$1$：若$x$为$0$，表示城市$a$不得驻扎军队，若$x$为$1$，表示城市$a$必须驻扎军队；若$y$为$0$，表示城市b不得驻扎军队，若$y$为$1$，表示城市$b$必须驻扎军队。 

输入文件中每一行相邻的两个数据之间均用一个空格分隔。

输出格式

输出共$m$行，每行包含$1$个整数，第$j$行表示在满足国王第$j$个要求时的最小开销，如果无法满足国王的第$j$个要求，则该行输出$-1$。

数据范围

$$ n,m \le 300000 \\\\ 1 \le p_i \le 100000 $$

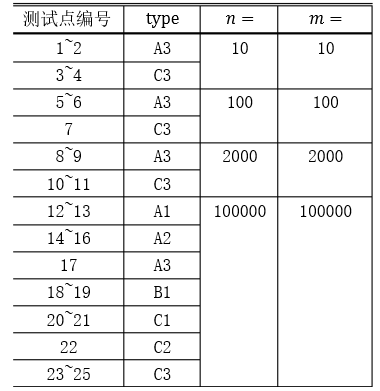
数据类型的含义： 

A：城市i与城市i+1直接相连。 
B：任意城市与城市1的距离不超过100（距离定义为最短路径上边的数量），即如果这棵树以1号城市为根，深度不超过100。 
C：在树的形态上无特殊约束。
1：询问时保证a=1,x=1，即要求在城市1驻军。对b,y没有限制。 
2：询问时保证a,b是相邻的（由一条道路直接连通） 
3：在询问上无特殊约束。

输入样例：

5 3 C3
2 4 1 3 9
1 5
5 2
5 3
3 4
1 0 3 0
2 1 3 1
1 0 5 0

输出样例：

12
7
-1

解题报告

题意理解

这道题目的意思其实,可以一句话概括,没有上司的舞会数据加强版…

如果说,详细地解说的话,就是.

一条边的两个端点,必须至少有一个点有军队驻扎.

要求所有的边都要合法,问最少的花费.

算法解析

这道题目 $\text{44pts}$ 其实还是挺好拿到的.

我们完全可以开一个 $O(NM)$ 时间复杂度的 树型DP ,强势求解.

我们这里主要讲解如何优化这道题目,来达到最终的 ${\color{green}{AC}}$ 的目的.

现在我们注意一下,题目给了我们哪些信息,或者说是性质,让我们来认真推理.

首先这道题目,其实给了我们不少有用的信息,比如说题目告诉我们.

1. 这道题目是 $\text{DP}$ ,也就是说这道题目的优化,与动态规划周边的优化,是有关系的.
2. 树 上面的优化
3. 每个询问 只影响两个 点

根据上面得到的信息,我们不难思考出来,这道题目应该和, 倍增优化 有一定的关系.

就然如此,我们不妨判断一下,这道题目,如何使用LCA的一大解决方案, 树上倍增 来优化本题.

通过树型DP,我们不难发现,其实除了我们每一次 询问 影响的两个点 以外 的点dp的过程其实没有 任何变化 .

接下来,我们主要来分析一下,就是我们如何通过上面这个非常重要的性质,来为我们确定一下,这道题目的 核心关键优化点 .

那么假如说,我们单独处理出, 除了这两个点以外的dp值 ,那么我们再处理这两个点,不就好了么?

但是这道题目的空间就会爆炸,从而让这道题目无解.

但是我们想一想,其实我们完全可以使用 倍增优化 空间&时间的.

因此,综上所述,我们现在主要思考,如何使用倍增优化这道题目.

我们先来回忆一下,之前是如何使用倍增优化LCA的.

开一个 fa 数组,然后fa[x][i]表示从x 节点开始出发,往上面跳跃 $2^i$ 个节点,得到的数值.

然后呢我们先来设置几个数组

$f[i][0/1]$ 表示选或不选$i$结点，选择以$i$为根的子树所有结点的最优值

$g[i][0/1]$ 表示的是选或不选$i$结点，整棵树除了以$i$为根的子树以外全部选择的最优值

那么如何将倍增的思想,运用到本题上来?

$dp[i][j][0/1][0/1]$ 表示的是$i$结点选或不选，$i$的$2^j$祖先$father$选或不选，以$father$为根的子树内独不选以i为根的子树的最优值

既然现在倍增的思想已经完美地体现了,那么我们现在的重点,就是 如何针对询问操作

其实我们发现,两个节点,他们可以影响地范围如下.

$a->Lca(a,b) \\\\ b->Lca(a,b)$

也就是说$a->b$的路径上的节点,才会被影响.

那么我们怎么处理呢?

回想一下, $\color{red}{Lca}$ 算法是怎么快速地处理的.

1. 两个节点跳跃到 同一高度
2. 如果两个节点存在 祖孙关系 那么跳跃到同一高度,直接输出
3. 倍增跳跃 直到到达$Lca$节点

然后我们不妨,在设置一个具体的数组.

$now_x[1/0]$ 表示为是否选取当前点的子树最优值.

其实也可以认为是,从$x$跳跃到这个节点的最优值.

同理也可以开一个.

$now_y[1/0]$来存储

这就是我们所有的思路了.

Update:
讲解的不是很好,希望大家见谅,因为黑夜降临,屏幕微亮,眼睛肿痛.

最后一句:表白暖萌的梁靖康,秦淮岸的精神支柱.

代码解析

#include <bits/stdc++.h>
#define read(x) scanf("%d",&x)
#define ll long long
using namespace std;
const int N=1e5+10;
const ll INF=1e16;
int n,m,val[N],deep[N],fa[N][18],head[N],edge[N<<1],Next[N<<1],tot;
ll f[N][2],g[N][2],w[N][18][2][2];
char op[10];
inline void add_edge(int x,int y)
{
    edge[++tot]=y;
    Next[tot]=head[x];
    head[x]=tot;
}
void dfs1(int x,int Fa)
{
    deep[x]=deep[Fa]+1;
    fa[x][0]=Fa;
    f[x][1]=val[x];
    for(int i=head[x],y; i; i=Next[i])
    {
        y=edge[i];
        if(y==Fa)
            continue;
        dfs1(y,x);
        f[x][0]+=f[y][1];
        f[x][1]+=min(f[y][0],f[y][1]);
    }
}

void dfs2(int x)
{
    for(int i=head[x],y; i; i=Next[i])
    {
        y=edge[i];
        if(y==fa[x][0])
            continue;
        g[y][0]=g[x][1]+f[x][1]-min(f[y][0],f[y][1]);
        g[y][1]=min(g[y][0],g[x][0]+f[x][0]-f[y][1]);
        dfs2(y);
    }
}

ll solve(int a,int x,int b,int y)
{
    if(deep[x]<deep[y])
        swap(x,y),swap(a,b);
    ll nx[2],ny[2],tx[2]= {INF,INF},ty[2]= {INF,INF};
    tx[a]=f[x][a];
    ty[b]=f[y][b];
    for(int i=17; i>=0; i--)
        if(deep[fa[x][i]] >= deep[y])
        {
            nx[0]=nx[1]=INF;
            for(int j=0; j<2; j++)
                for(int k=0; k<2; k++)
                    nx[j]=min(nx[j],tx[k]+w[x][i][k][j]);
            tx[0]=nx[0];
            tx[1]=nx[1];
            x=fa[x][i];
        }
    if(x==y)
        return tx[b]+g[y][b];
    for(int i=17; i>=0; i--)
        if(fa[x][i] != fa[y][i])
        {
            nx[0]=nx[1]=ny[0]=ny[1]=INF;
            for(int j=0; j<2; j++)
                for(int k=0; k<2; k++)
                {
                    nx[j]=min(nx[j], tx[k]+w[x][i][k][j] );
                    ny[j]=min(ny[j], ty[k]+w[y][i][k][j] );
                }
            tx[0]=nx[0];
            tx[1]=nx[1];
            x=fa[x][i];
            ty[0]=ny[0];
            ty[1]=ny[1];
            y=fa[y][i];
        }
    int lca=fa[x][0];
    ll ans1=f[lca][0]-f[x][1]-f[y][1]+tx[1]+ty[1]+g[lca][0];
    ll ans2=f[lca][1]-min(f[x][0],f[x][1])-min(f[y][0],f[y][1])+min(tx[0],tx[1])+min(ty[0],ty[1])+g[lca][1];
    return min(ans1,ans2);
}
inline void init()
{
    read(n),read(m);
    scanf("%s",op);
    for(int i=1; i<=n; i++)
        read(val[i]);
    for(int i=1; i<n; i++)
    {
        int x,y;
        read(x),read(y);
        add_edge(x,y);
        add_edge(y,x);
    }
}
inline void prework()
{
    dfs1(1,0);
    dfs2(1);
    for(int i=1; i<=n; i++)
    {
        int now=fa[i][0];
        w[i][0][0][0]=INF;
        w[i][0][0][1]=f[now][1]-min(f[i][0],f[i][1]);
        w[i][0][1][0]=f[now][0]-f[i][1];
        w[i][0][1][1]=w[i][0][0][1];
    }
    for(int j=1; j<=17; j++)
        for(int i=1; i<=n; i++)
        {
            int now=fa[i][j-1];
            if(fa[now][j-1])
            {
                fa[i][j]=fa[now][j-1];
                for(int u=0; u<2; u++)
                    for(int v=0; v<2; v++)
                    {
                        w[i][j][u][v]=INF;
                        for(int k=0; k<2; k++)
                            w[i][j][u][v]=min(w[i][j][u][v],w[i][j-1][u][k]+w[now][j-1][k][v]);
                    }
            }
        }
}
inline void work()
{
    while(m--)
    {
        int x,a,y,b;
        read(x),read(a),read(y),read(b);
        if(!a && !b && (x==fa[y][0] || y==fa[x][0]))
        {
            printf("-1\n");
            continue;
        }
        printf("%lld\n",solve(a,x,b,y));
    }
}
int main()
{
    init();
    prework();
    work();
    return 0;
}

感谢洛水·锦依卫大佬的博客