$ $ 友情提醒，小白慎进

我发现了这个题目的一个规律

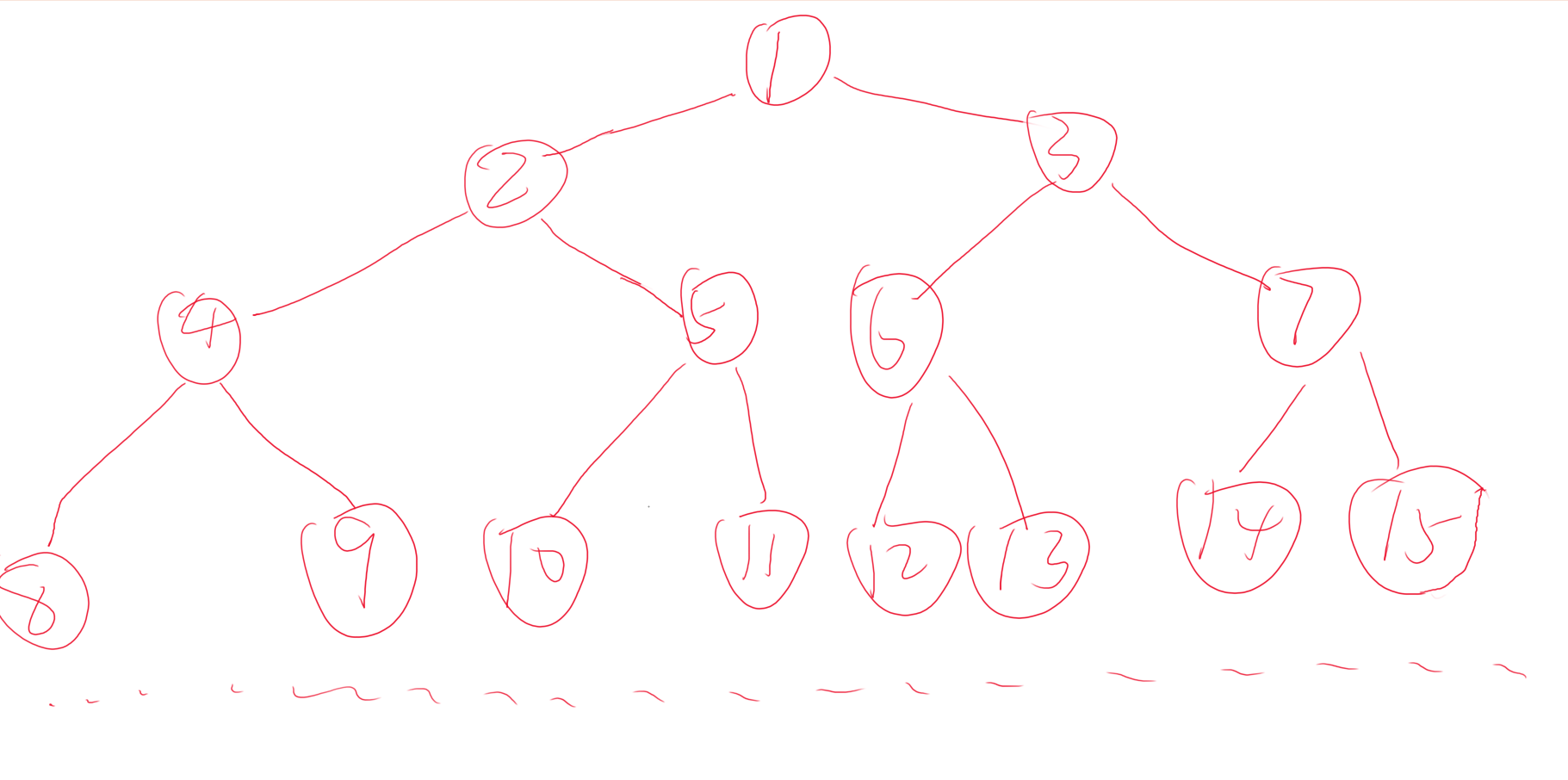
每个深度的点是固定的而且规律很好找！

1、那好了，那这题就成了一道规律题，我们只需要根据这个规律计算每一层的大小然后比较、记录就好了。

2、规律是，第 $i$ 层，就有 $2^{i-1}$ 个节点。

3、那么我们把每个节点加起来，就是这层的权值

4、然后用擂台法比较、记录

5、最后输出

6、当然了这里涉及到一个计算每层的问题，因为每一层的起始位置是不一样的，所以我们要顶一个位置来记录一下我们当前应该从哪一个位置开始加

7、然后对应好每一层加多少个就好了

代码里面会解释的哦！

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<climits>

using namespace std;

const int N=1000010;

int n;

int a[N];

int main()
{
    scanf("%d",&n);

    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
    }

    int max_=INT_MIN;//用于擂台法比较，记录最大值，一开始要小一些

    int k=1;

    int weizhi=1;//记录当前应该从哪个位置开始计算
    for(int i=0;i<=1000;i++)
    {
        long long sum=0;//计算每一层的总和
        for(int j=weizhi;j<=(1<<i)+weizhi-1;j++)//i<<i 等价于pow(2,i)
        {
            sum+=a[j];//求和
        }

        weizhi+=1<<i;//更新一下当前的位置
        if(sum>max_)//如果我们当前的和严格大于维护的最大值，就更新一下，注意是严格大于，因为题目说了二者相等时输出最小的深度
        {
            k=i+1;//由于 i 从0开始的所以我们要 +1
            max_=sum;
        }

        if(weizhi>=n)//如果我们当前位置大于 n 了，那就退出
        break;

    }

    printf("%d",k);//输出目标值

    return 0;
}

本解法仅供参考，大家请用y总教的做法，谢谢！！（别忘了点赞亲~）