题目描述

题目描述
有一个长方形的房间，铺着方形瓷砖。每块瓷砖都涂上红色或黑色。一个男人站在黑色的瓷砖上。从瓦片，他可以移动到四个相邻的瓷砖之一。但他不能在红瓦上移动，他只能在黑瓦上移动。

编写一个程序，通过重复上述步骤来计算他可以达到的黑色瓷砖的数量。
输入
输入由多个数据集组成。数据集以包含两个正整数W和H的行开始; W和H分别是x方向和y方向上的瓦片数量。W和H不超过20.
数据集中有更多的行，每个行包含W个字符。每个字符表示一个瓦片的颜色如下。
‘.’ – 黑色瓦片
‘＃’ – 红色瓦片
‘@’ –黑色瓦片上的男士（在数据集中恰好出现一次）
输入的末尾由包含两个零的行表示。

输出
对于每个数据集，程序应该输出一行，其中包含他可以从初始图块（包括自身）到达的图块数量。

样例

输入样例：

6 9 
....#. 
.....# 
...... 
...... 
...... 
...... 
...... 
#@...# 
.#..#. 
0 0

输出样例：

45

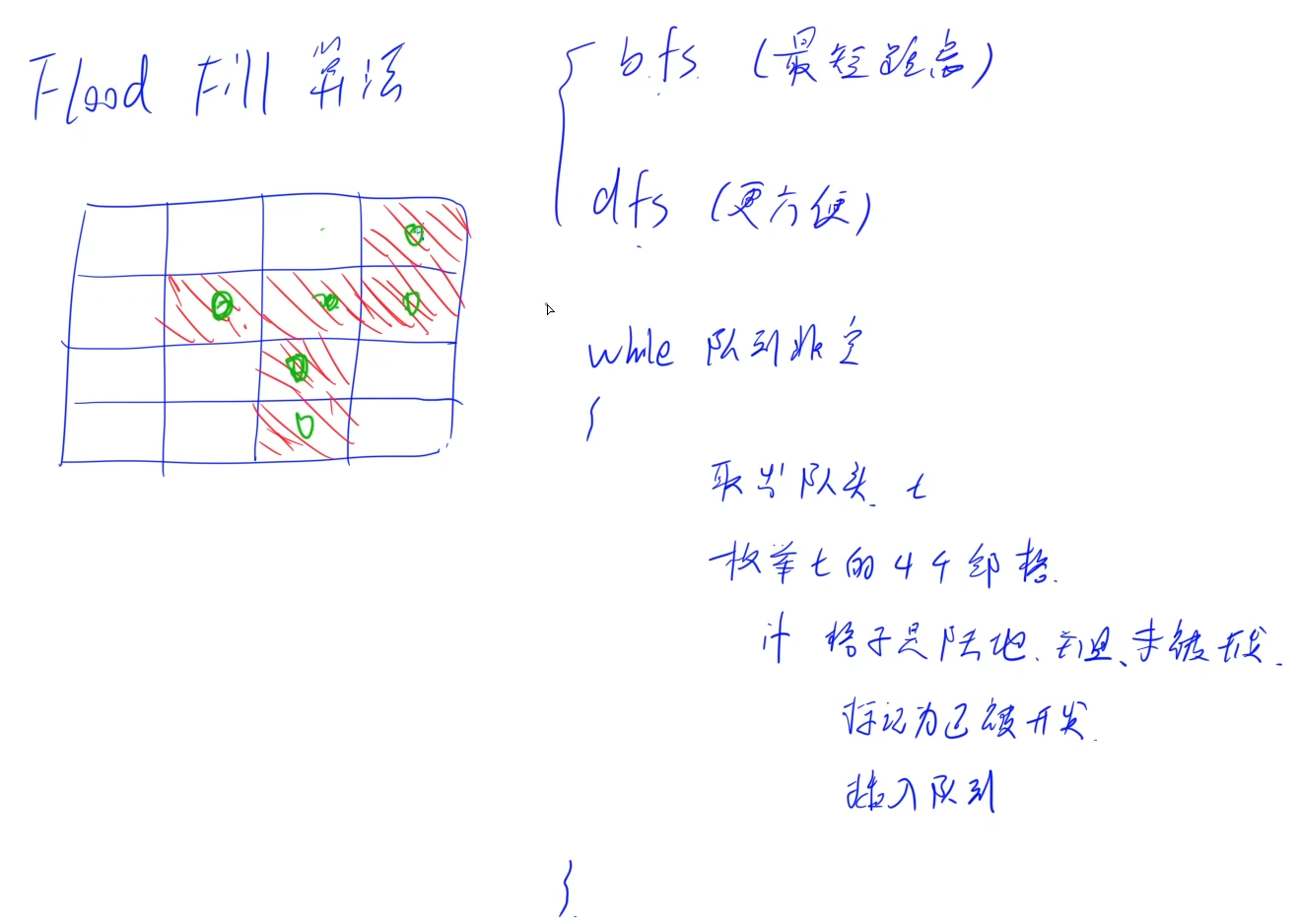
dfs代码短，更方便
bfs第一次搜到的肯定距离最短,一层一层的走
在以后的做题中，让求最小步数的时候用bfs,其他都用dfs

dfs:

深搜递归

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int r,c;
int fx[5]={0,0,1,-1},fy[5]={1,-1,0,0};
char mapp[25][25]; 
int s=0;
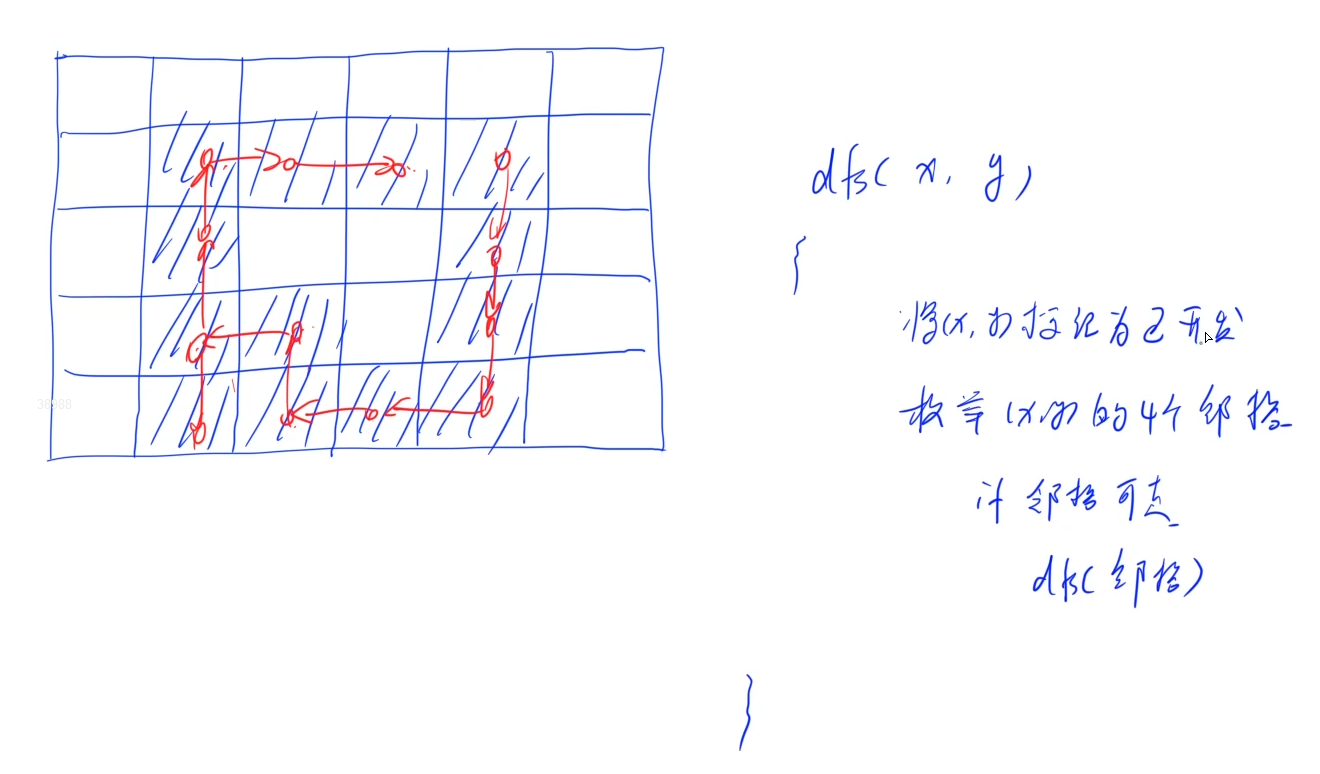
void dfs(int x,int y){
    mapp[x][y]='#';//走过的‘.’就立即标为‘#‘，省的重复算了，再者多样例时不用数组清0了，因为反正赋值为’#‘了，不会跟结果有冲突的，反正是只走’.‘ 
    s++;//包括自身
    for(int i=0;i<4;i++){
        int a=x+fx[i];
        int b=y+fy[i];
        if(a>0&&a<=c&&b>0&&b<=r&&mapp[a][b]=='.'){
            dfs(a,b);
        }
    }
}
int main(int argc, char** argv) {
    int flag=0;
    while(cin>>r>>c&&r!=0&c!=0){
        s=0;
        int i,j;
        for(i=1;i<=c;i++){
        for( j=1;j<=r;j++){
            cin>>mapp[i][j];
        }
    }
    flag=0;
    for( i=1;i<=c;i++){
        for(j=1;j<=r;j++){
            if(mapp[i][j] == '@'){
                flag=1;
                break;
            }
        }
        if(flag) break;
    }
    dfs(i,j);
    cout<<s<<endl;
    }

    return 0;
}

*bfs:

宽搜队列先进先出

#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
#include <algorithm>
#define x first
#define y second
using namespace std;
typedef pair<int,int> PII;
int r,c;
char mapp[25][25];
int cnt;
int fx[5]={0,0,1,-1},fy[5]={1,-1,0,0};
queue<PII> q;
void bfs(int x,int y){
    mapp[x][y]='#'; 
    q.push({x,y});
    while(!q.empty()){
        PII t=q.front();//取队头 
        q.pop();//删除队头元素 
        cnt++;
        for(int i=0;i<4;i++){
            int a=t.x+fx[i];
            int b=t.y+fy[i];
            if(a<0||a>=c||b<0||b>=r||mapp[a][b]!='.') continue;
            q.push({a,b});//合法就入队
            mapp[a][b]='#';//标记一下遍历入队过了，下次不再入队
        }
    }
}
int main(int argc, char** argv) {
    while(cin>>r>>c&&r!=0&&c!=0){
        cnt=0;
        for(int i=0;i<c;i++){
        for(int j=0;j<r;j++){
            cin>>mapp[i][j];
        }
    }
    int flag=0;
    for(int i=0;i<c;i++){
        for(int j=0;j<r;j++){
            if(mapp[i][j]=='@'){
                bfs(i,j);
                printf("%d\n",cnt); 
                flag=1;
                break;
            }
        }
        if(flag){
            break;
        }
    }
    }
    return 0;
}