• 仅供自己复习用
  官方题解: https://codeforces.com/blog/entry/89007
  A.题意：求出纵序矩形某座标在行序矩形中代表的数
  解法: 求出行与列即可 行 = x % n 列 = x / 3

B.题意：

C.题意求将a, b串变成相同的串所需要的最小步数
解法:LCS问题 – 最长公共子串问题

求两个串的最长公共子串的方法

法一：暴力

for(int len = 1; len <= min(a.size(), b.size()); len ++ ) {
        for(int j = 0; j + len <= a.size(); j ++ ) {  /*attention: <= a.size()  remember =*/
                                                      /* <==> [ , ) */ 
            for(int k = 0; k + len <= b.size(); k ++ ) {
                if(a.substr(j, len) == b.substr(k, len)) {
                    ans = max(ans, len);
                }
            }
        }
    } 

法二：优雅的暴力 – 参考csdn




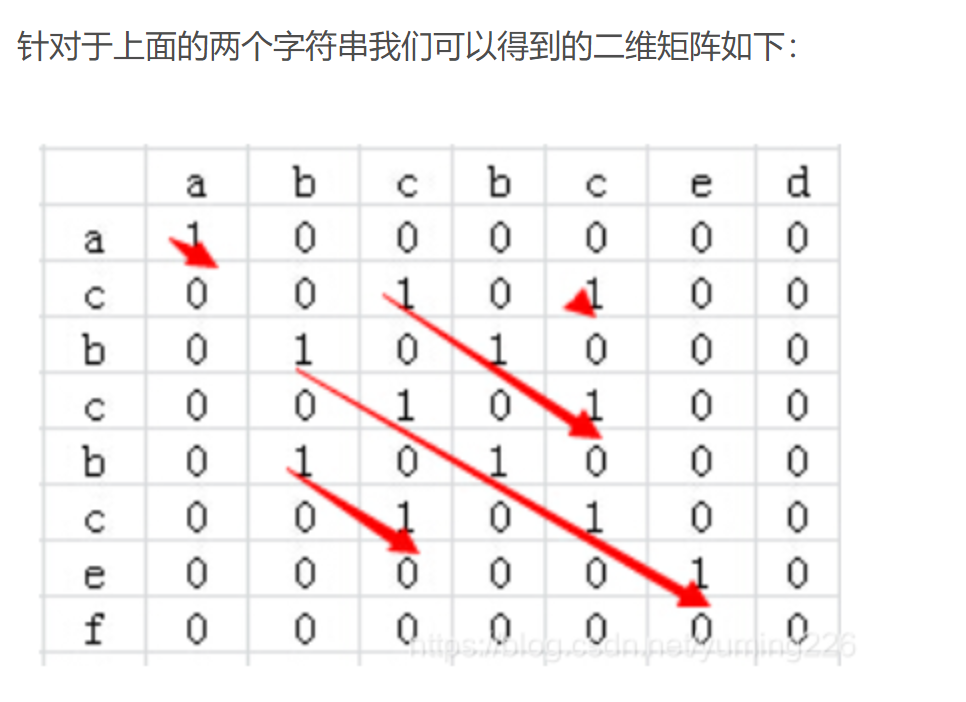
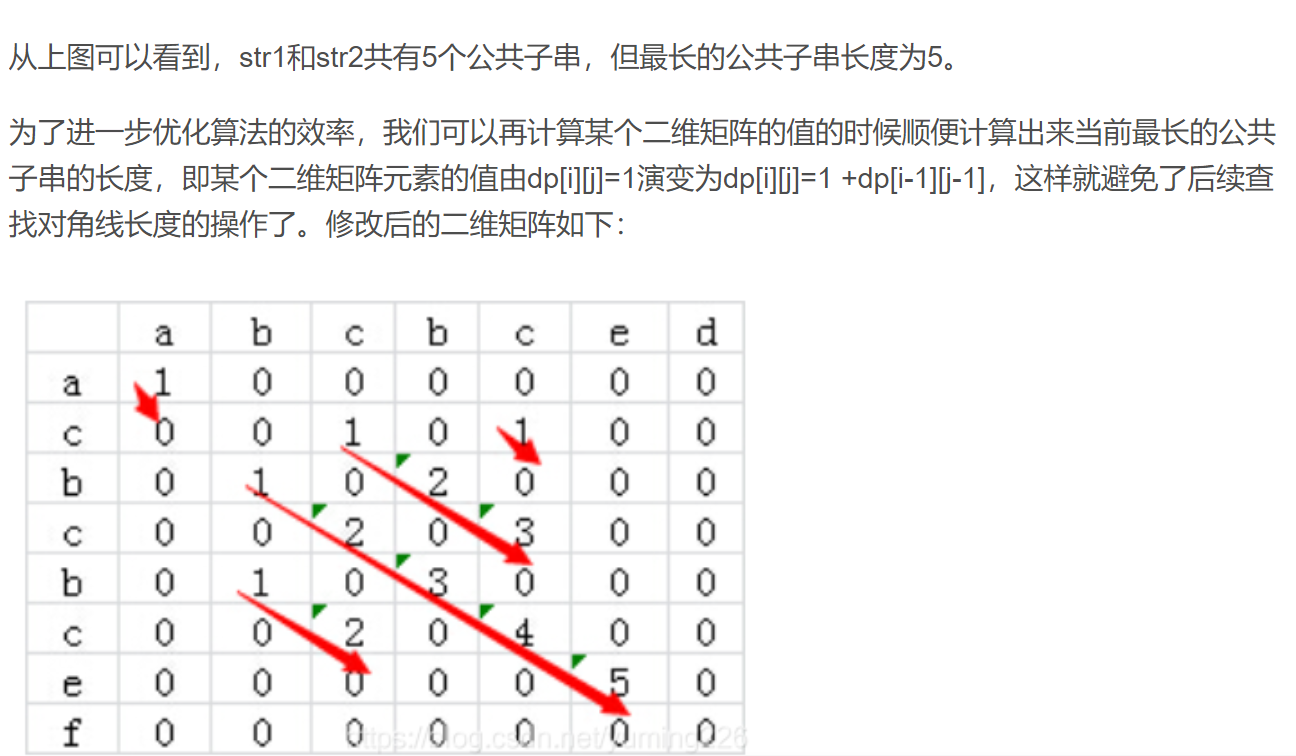
复杂度 – O(n^2)
AC代码：递推(类似dp)

#include <bits/stdc++.h>

using namespace std;
const int N = 30;
int t;
int len[N][N]; //在(i, j)位置的对角线的长度

int main() {
    cin >> t;
    while(t -- ) {
        int maxn = 0;   //最大对角线的长度
        memset(len, 0, sizeof len); 
        string a, b; cin >> a >> b;
        int n = a.size(), m = b.size();

        for(int i = 0; i < n; i ++ ) {
            for(int j = 0; j < m; j ++ ) {
                if(a[i] == b[j] && (i == 0 || j == 0)) {
                    len[i][j] = 1;
                    maxn = max(maxn, len[i][j]);
                }
                else if(a[i] == b[j]) {
                    len[i][j] = len[i - 1][j - 1] + 1;
                    maxn = max(maxn, len[i][j]);
                }
            }
        }

        cout << n + m - 2 * maxn << endl; 
    }

    return 0;
} 

D题：解法 贪心，每次选择数组中出现最多和出现第二多的数，选择最多的两个数可以最大限度的减小此次操作对数字种类的减少，通过priority_queue获取每次操作后的最值

#include <bits/stdc++.h> 
#define pque priority_queue
#define fir first
#define sec second
#define vi vector<int>

using namespace std;
const int N = 2e5 + 10;
int t, n;
int a[N]; 
map<int, int> mp;

int main() {
    cin >> t;
    while(t -- ) {
        mp.clear();
        cin >> n;
        for(int i = 1; i <= n; i ++ ) {
            cin >> a[i]; mp[a[i]] ++ ;
        }

        pque<int, vi> que;
        for(auto tmp : mp)  que.push(tmp.sec);

        if(que.size() == 1) {
            cout << que.top() << endl;
            continue;
        }

        while(que.size() > 1) {
            int maxn1 = que.top(); que.pop();
            int maxn2 = que.top(); que.pop();
            maxn1 -- , maxn2 -- ;
            if(maxn1) que.push(maxn1);
            if(maxn2) que.push(maxn2);
        }
        if(que.size()) cout << que.top() << endl;
        else cout << 0 << endl;
    }

    return 0;   
}