题目描述

很久以前，T王国空前繁荣。

为了更好地管理国家，王国修建了大量的快速路，用于连接首都和王国内的各大城市。

为节省经费，T国的大臣们经过思考，制定了一套优秀的修建方案，使得任何一个大城市都能从首都直接或者通过其他大城市间接到达。

同时，如果不重复经过大城市，从首都到达每个大城市的方案都是唯一的。

J是T国重要大臣，他巡查于各大城市之间，体察民情。

所以，从一个城市马不停蹄地到另一个城市成了J最常做的事情。

他有一个钱袋，用于存放往来城市间的路费。

聪明的J发现，如果不在某个城市停下来修整，在连续行进过程中，他所花的路费与他已走过的距离有关，在走第x千米到第x+1千米这一千米中（x是整数），他花费的路费是x+10这么多。也就是说走1千米花费11，走2千米要花费23。

J大臣想知道：他从某一个城市出发，中间不休息，到达另一个城市，所有可能花费的路费中最多是多少呢？

输入格式
输入的第一行包含一个整数 n，表示包括首都在内的T王国的城市数。

城市从 1 开始依次编号，1 号城市为首都。

接下来 n−1 行，描述T国的高速路（T国的高速路一定是 n−1 条）。

每行三个整数 Pi,Qi,Di，表示城市 Pi 和城市 Qi 之间有一条双向高速路，长度为 Di 千米。

输出格式
输出一个整数，表示大臣J最多花费的路费是多少。

数据范围
$1≤n≤10^5,$
$1≤P_i,Q_i≤n ,$
$1≤D_i≤1000$
输入样例：

5 
1  2  2 
1  3  1 
2  4  5 
2  5  4

输出样例：

135

算法1

思路：

• 由于题目中说 任何一个大城市都能直接或间接到达，如果不经过重复的大城市，则首都到达每个大城市的路径唯一，那么根据这同样的性质，可以将城市与首都之间抽象成一个无环连通图，即为一棵树

• 参考树的直径的定义，了解树的直径，该怎样求树的直径

• 两遍dfs求树的直径

分析：

• 这个题是怎样的转化为求树的直径的：

聪明的J发现，如果不在某个城市停下来修整，在连续行进过程中，
他所花的路费与他已走过的距离有关，在走第x千米到第x+1千米这一千米中（x是整数）
他花费的路费是x+10这么多。也就是说走1千米花费11，走2千米要花费23

• 仔细阅读题目将数据打表，不难发现这样的规律

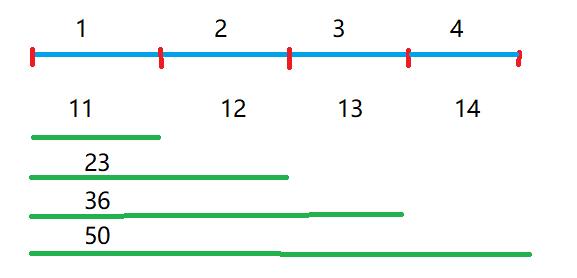
假设走了s千米远,那么总花费 $ W = 10 + 10 + 1 + 10 + 2 + 10 + 3 + ...... + 10 + s$ 整理得:
$$ W = 10·s + \frac{s·(s + 1)}{2} $$
可以看出W是根据s单调递增的，所以s越大W越大

• 根据以上分析就可以确定当树中任意两点间距离最长那么花费就一定最多，现在就是考虑如何求得最长的路径的，可以发现树的直径刚好满足这样的性质，那怎样求得树的直径呢

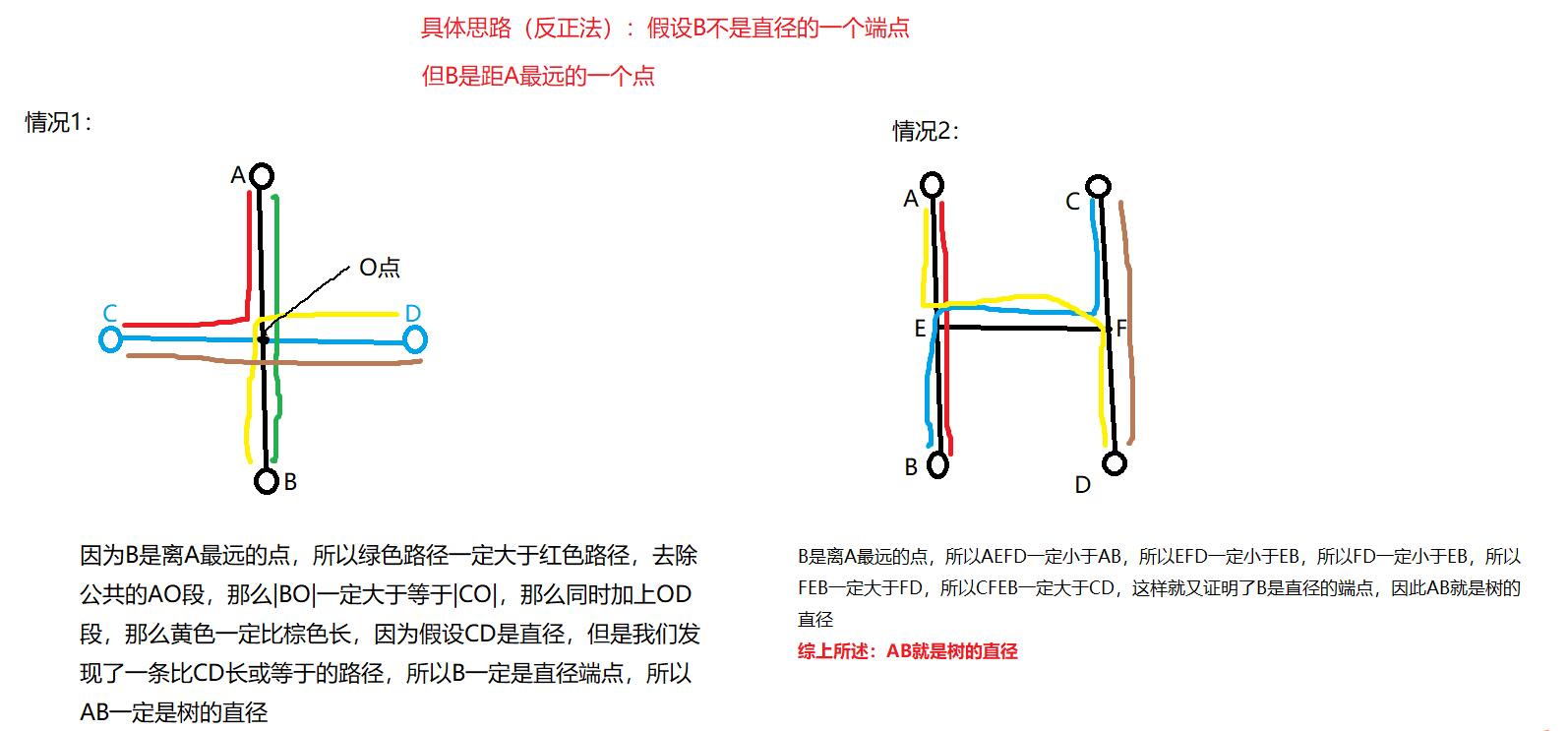
• 可以考虑的是，任取图中一个节点，找到离这个节点最远的节点，在去寻找离那个最远节点的最远节点，这样两个最远节点之间就是树的路径了， 具体证明看图

• 分析到这里就可codeing了

c++代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>

using namespace std;
const int N = 100010, M = 2 * N;

int n;
int h[N], e[M], w[M], ne[M], idx;
int dist[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

void dfs(int u, int father, int distance)
{
    dist[u] = distance;
    for(int i = h[u]; i != -1 ; i = ne[i])
    {
        int j = e[i];
        if(j != father)
            dfs(j, u, distance + w[i]);
    }
}

int main()
{
    scanf("%d", &n);
    memset(h, -1, sizeof h);

    for(int i = 0; i < n - 1; i ++ )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }

    dfs(1,-1, 0);
    int u = 1;
    for(int i = 2; i <= n; i ++ )
        if(dist[u] < dist[i])
            u = i;
    dfs(u, -1, 0);

    for(int i = 1; i <= n; i ++ )
        if(dist[u] < dist[i])
            u = i;

    long long res = dist[u] * 10 + (dist[u] + 1ll) * dist[u] / 2;
    printf("%lld", res);
    return 0;
}