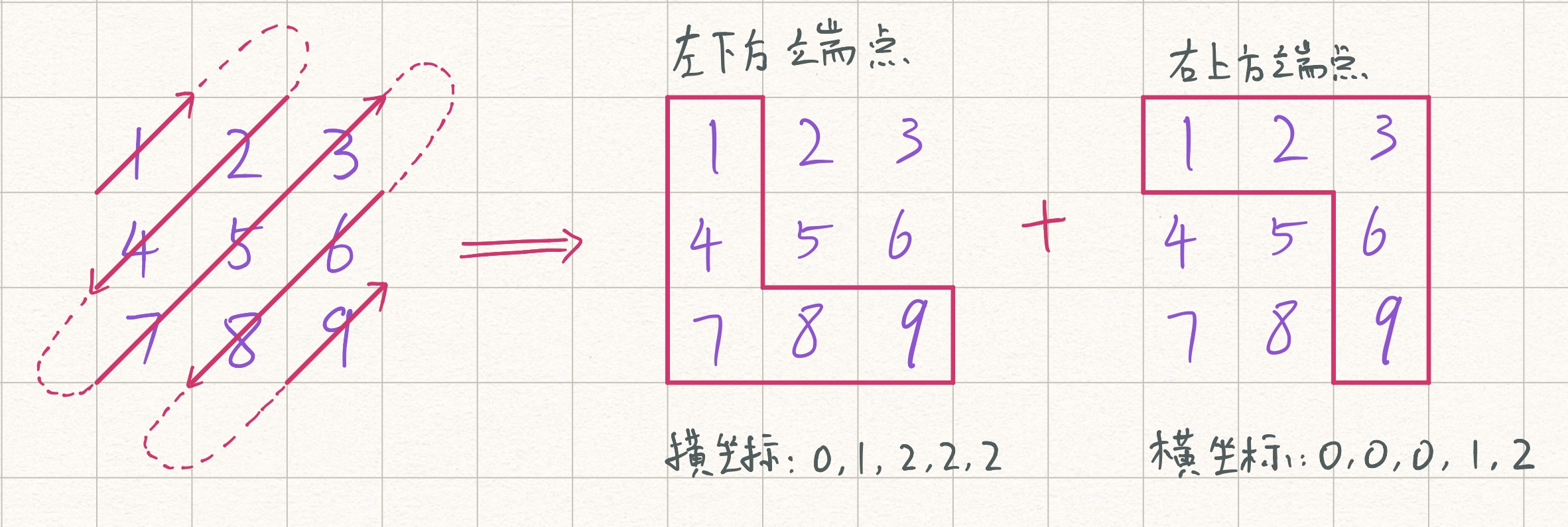
正对角线有一个性质：同一条对角线上每个点的(x，y)坐标之和相等。通过观察易知矩阵一共有 m + n - 1 条对角线，每条对角线要么从左下到右上，要么从右上到左下，先求出这两个端点，再根据当前循环的方向进行遍历。
根据对角线性质，只要知道端点的横纵坐标之一，就可以得到另一维坐标，图例中我们只关心横坐标。

class Solution {
public:
    vector<int> findDiagonalOrder(vector<vector<int>>& matrix) {
        if (matrix.empty() || matrix[0].empty()) return {};

        vector<int> res;
        int n = matrix.size(), m = matrix[0].size();
        int direction = 1;

        for (int s = 0; s < n + m; ++ s)
        {                                       //right_up为右上端点横坐标,left_down为左下端点横坐标
            int right_up = max(0, s - m + 1);   //s < m 时用 0，s > m + 1 时用 s - m + 1
            int left_down = min(s, n - 1);      //s < n 时用 i，s >= n 时用 n - 1
            if (direction)                      //dicection = 1 为左下往右上方向
            {
                for (int x = left_down; x >= right_up; -- x)    //左下往右上时，横坐标是逐渐变小的
                    res.push_back(matrix[x][s - x]);            //知道横坐标，可得纵坐标
            }
            else
            {
                for (int x = right_up; x <= left_down; ++ x)    //右上往左下时，横坐标是逐渐变大的
                    res.push_back(matrix[x][s - x]);
            }

            direction ^= 1;                                     //每次循环变换方向
        }

        return res;
    }
};