树的遍历 + BFS

时间复杂度 $O(N)$

注意：

1、给定 前序、中序遍历，可求 后序、层序遍历。
2、给定 后序、中序遍历，可求 前序、层序遍历。
3、给定 前序、后序遍历，无法唯一确定 中序、层序遍历（因为有 前序和后序遍历 重复信息）。

已知 中序和后序遍历，求解 层序遍历。

思路：

我们需要利用 中序和后序遍历 建立一颗二叉树，对二叉树进行 BFS 即可，核心就在于如何建树。

中序遍历的顺序：左->根->右，后序遍历的顺序：左->右->根，先用哈希表将中序遍历的每个元素的位置记录下来，方便后续查找后序遍历的根在中序遍历中的位置，以此划分中序、后序当前根的左右子树，再不断的左、右递归建树。

示意图如下：

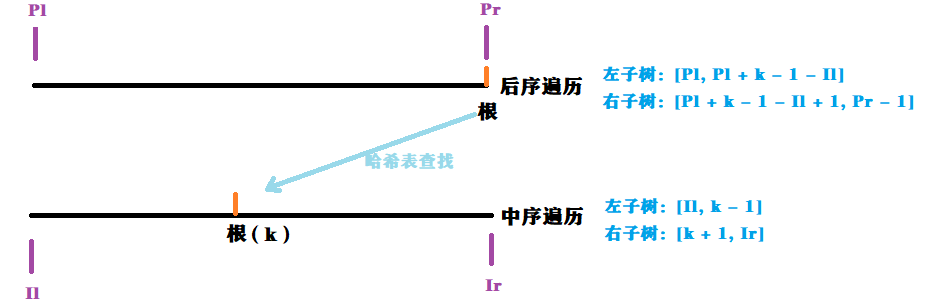
当树建好后，只需对得到的 L[]、R[] 进行 BFS 即可得到层序遍历。

因为每个节点只被遍历了一次，所以时间复杂度为 $O(N)$。

C++ 代码

#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
#include <unordered_map>
using namespace std;

const int N = 40;
int n;
int postorder[N], inorder[N];
unordered_map<int, int> l, r, pos;

// 后序遍历：左右根
// 中序遍历：左根右

int build(int il, int ir, int pl, int pr)
{
    int root = postorder[pr];
    int k = pos[root]; // 根节点在中序遍历中位置
    if (il < k) l[root] = build(il, k - 1, pl, pl + k - 1 - il); // 左子树
    if (ir > k) r[root] = build(k + 1, ir, pl + k - 1 - il + 1, pr - 1); // 右子树
    return root;
}

void bfs(int root) // bfs 实现层序遍历
{
    queue <int> q;
    q.push(root);
    while (!q.empty()) { 
        int t = q.front();
        q.pop();
        cout << t << ' ';
        if (l[t]) q.push(l[t]);
        if (r[t]) q.push(r[t]);
    }
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; ++i) cin >> postorder[i];
    for (int i = 0; i < n; ++i) {
        cin >> inorder[i];
        pos[inorder[i]] = i; // 记录中序遍历中每个点的位置
    }
    int root = build(0, n - 1, 0, n - 1); // 重建 二叉树
    bfs(root);
    return 0;
}